本笔记内容或有错误，仅供参考
本文 All Right Reserved 保留所有权利，禁止商用和任何形式的转载!

AP 各学科「速成」笔记导览

Unit 1: Electronics

Electrostatics 静电

Charge 电荷

• 正（Positive） / 负（Negative） 电荷
• 元电荷（Elementary Charge） \(e = 1.6\times 10^{-19}\text{c}\)
  • 其中 \(\text{c}\) 为国际单位 库仑
• 电荷是守恒的，不会凭空产生也不会凭空消失，只可能从一个地方移动到另一个地方

Polarization and Induced Charges 极化和诱导带电

• 如图所示, C 带正电荷, 棍子的左半部分就会被诱导带负电荷，右边的部分就会被诱导带正电荷，但整体是电中性（也就是不带电）的
• 若此时将中间断开，那么左半部分整体就会带负电（而不是电中性），右半部分亦然

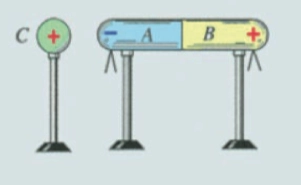
• 2015 AP: C, 整个圆球是不带电的，电荷守恒
  • 若支架为导体，答案为何？
    • 将圆球和支架视为一个整体，不难发现，这是一个竖直导体，当左边的棒子诱导带电，竖直导体的上半部分（也就是圆球），会带正电，而下半部分就会带负电。
    • 所以答案会变成 A.
  • 若左边的棒子直接接触圆球会怎样？
    • 所有来自棒子的负电荷都会转移到球形导体上，使球体带负电荷。

Coulomb’s Law 库仑定律

• 库仑定律（Coulomb’s Law）定义了，若两个带电粒子之间的电荷量为 \(q_1\) 和 \(q_2\) ，相隔距离为 \(r\)，则两电荷作用力为:

\[ F = k \frac{q_1q_2}{r^{2}} \]

其中 \(k = \frac{1}{4\pi \epsilon_0}\)

Compared to the Gravitation 与重力的比较

\[ F_G = G \frac{m_1m_2}{r^{2}} \quad F_E = k \frac{q_1q_2}{r^{2}} \]

• 观察重力的公式
  • 相似性: 形式上, 力都正比于距离的平方分之一（也就是反比于距离的平方） \(F \propto \frac{1}{r^2}\)
  • 不同: 方向不同（取决于电荷符号）, 大小不同（\(G\) 和 \(k\) 的巨大差异）

Superposition 叠加

• 向量（Vector）加法，不过多赘述

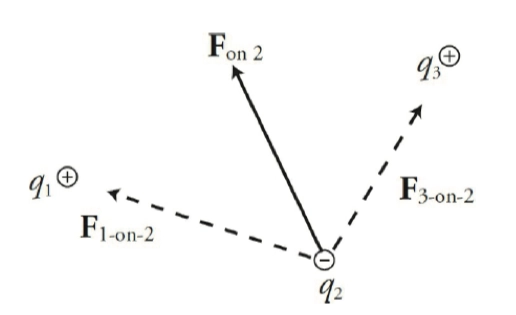
• 2016 AP: C

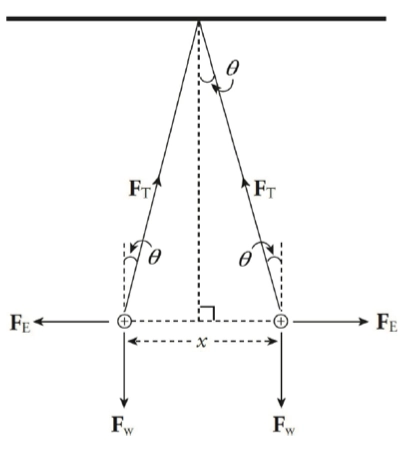
• 与 -Q 之间的距离是长于与两个 +Q 之间的距离的（三角形斜边大于其他两边），所以经过力的合成我们可以很显然的得到答案为 C

• Crack AP FRQ: 两个质量为 \(m\) 的小球分别带有电荷 \(+q\)。 他们以如图所示的方式，通过长度为 \(L\) 的细绳悬挂起来，并且因为相互的斥力隔开了一段距离。找到可以使得他们最终达到平衡的距离 \(x\)，以 \(m\), \(q\) 和 \(L\) 的形式表达。 (提示：若 \(\theta\) 很小， 那么 $$)

• 此题仅作思考，答案自寻

• Three Charge Superposition 三个点电荷共线平衡问题

  • 结论
    • 方向交替（也就一定是 正负正，或者 负正负）
    • 两边的电荷量一定大于中间的

Semicircle Model Practice 半圆模型

• Crack AP FRQ: 一个细导体均匀地带有电荷，密度为 \(\lambda = Q / L\)，然后将这个细导体弯成半径为 \(R\) 的半圆, 将一个电荷 \(+Q\) 放到该半圆的中心。计算该电荷所受到的电磁力。

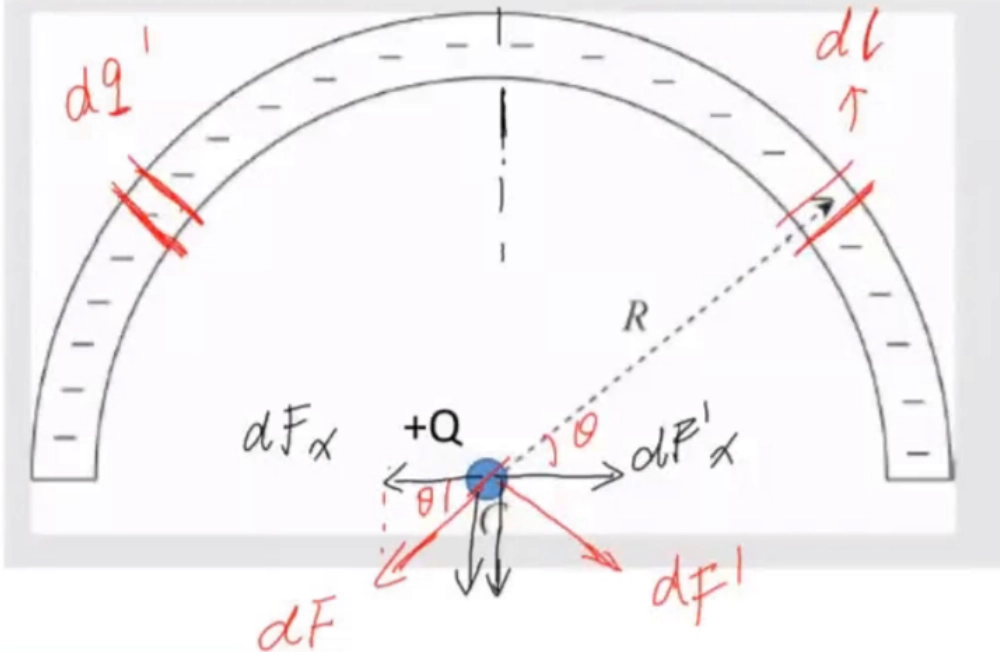
• 由于该问题并不是简单的点电荷，而是一段连续体，所以我们优先考虑一小段电荷 \(\mathrm{d}q\) 所产生的力 \(\mathrm{d}F\)
• 其次，问题具有良好的对称性，这意味着其水平方向上力的分量均可以被相互抵消，从而只需要计算竖直方向上的分量 \(\mathrm{d}F_y\)
• 我们依据库仑定律 \(F = k \frac{q_1q_2}{r^{2}}\) 写出 \(\mathrm{d}F_y\) 的表达式

\[ \mathrm{d}F_y = k\cdot \frac{Q\cdot \mathrm{d}q}{R^{2}} \sin \theta \]

• 继续计算 \(\mathrm{d}q\)，因为要统一到一个便于计算的微分量

\[ \mathrm{d}q = \lambda\cdot \mathrm{d}l = \lambda R\cdot \mathrm{d} \theta \]

• 最终得到

\[ \begin{aligned} F_{\text{net}} &= \int \mathrm{d}F_y \\ &= \int_{0}^{\pi } k\cdot \frac{Q \lambda }{R} \sin \theta ~\mathrm{d}\theta \\ &= k\cdot \frac{Q \lambda }{R} \cdot \int_{0}^{\pi } \sin \theta ~\mathrm{d}x \\ &= k\cdot \frac{Q \lambda }{R} \left\vert \cos \theta \right\vert^{\pi }_0 \\ &= k\cdot \frac{2Q \lambda }{R} = \frac{Q \lambda }{2 \pi \epsilon_0} \end{aligned} \]

Motion 运动

• 如果有一些电荷粒子被放置在图中位置，左上角的 -Q 的运动状态是什么，最后的运动位置是什么？

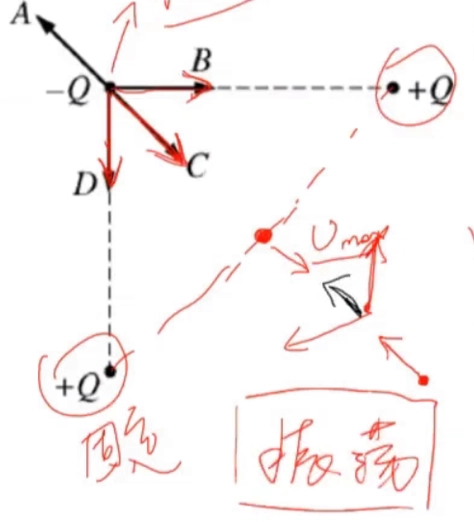
• -Q 粒子在到达两个 +Q 粒子之间的线时将停止运动，如果我们考虑到 -Q 的惯性，粒子可能会超过线一点点，并开始震荡。

Fields 电场

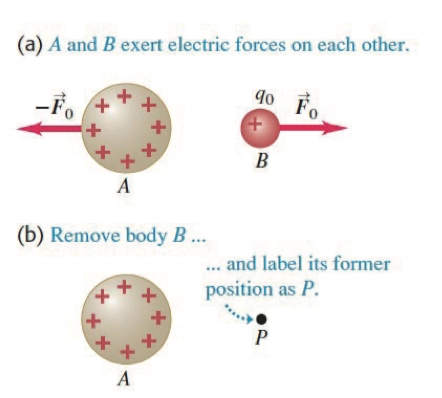
• 当空旷空间中的两个带电粒子相互作用时，每个粒子如何知道另一个粒子的存在？
• 就像万有引力一样，即使我们去掉粒子B，粒子A仍然在提供电场力，我们希望即使在我们不提供另外一个粒子的情况下，仍然能考虑和计算 A 提供的力，而这通常是一个范围，我们便称之为电场。

• 电场的公式如下，

\[ \vec{\mathbf{E}} = \frac{\vec{\mathbf{F}}}{q} \quad \vec{\mathbf{F}} = q \vec{\mathbf{E}} \]

• 注意：这只是电场的定义式，而不是决定式

\[ \vec{\mathbf{E}} = k \frac{q}{r^{2}} \]

• 电场的方向如下：

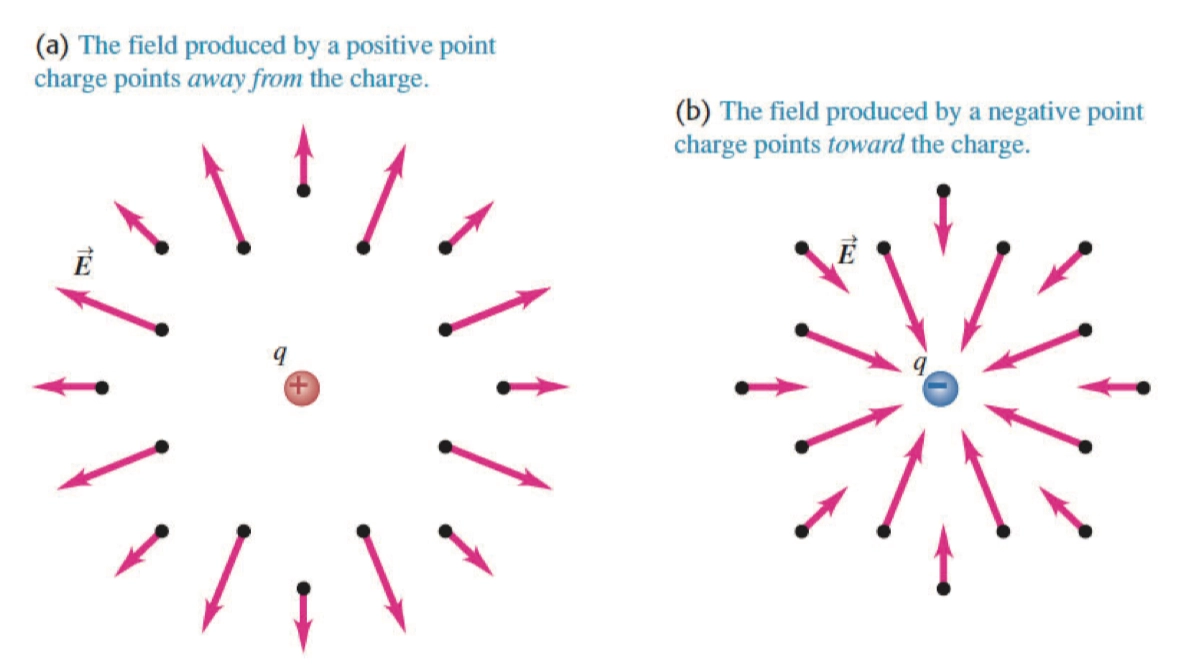
• 电场线 是用于描述电场，虚拟的线

Electric Dipole Practice 电偶极子的练习

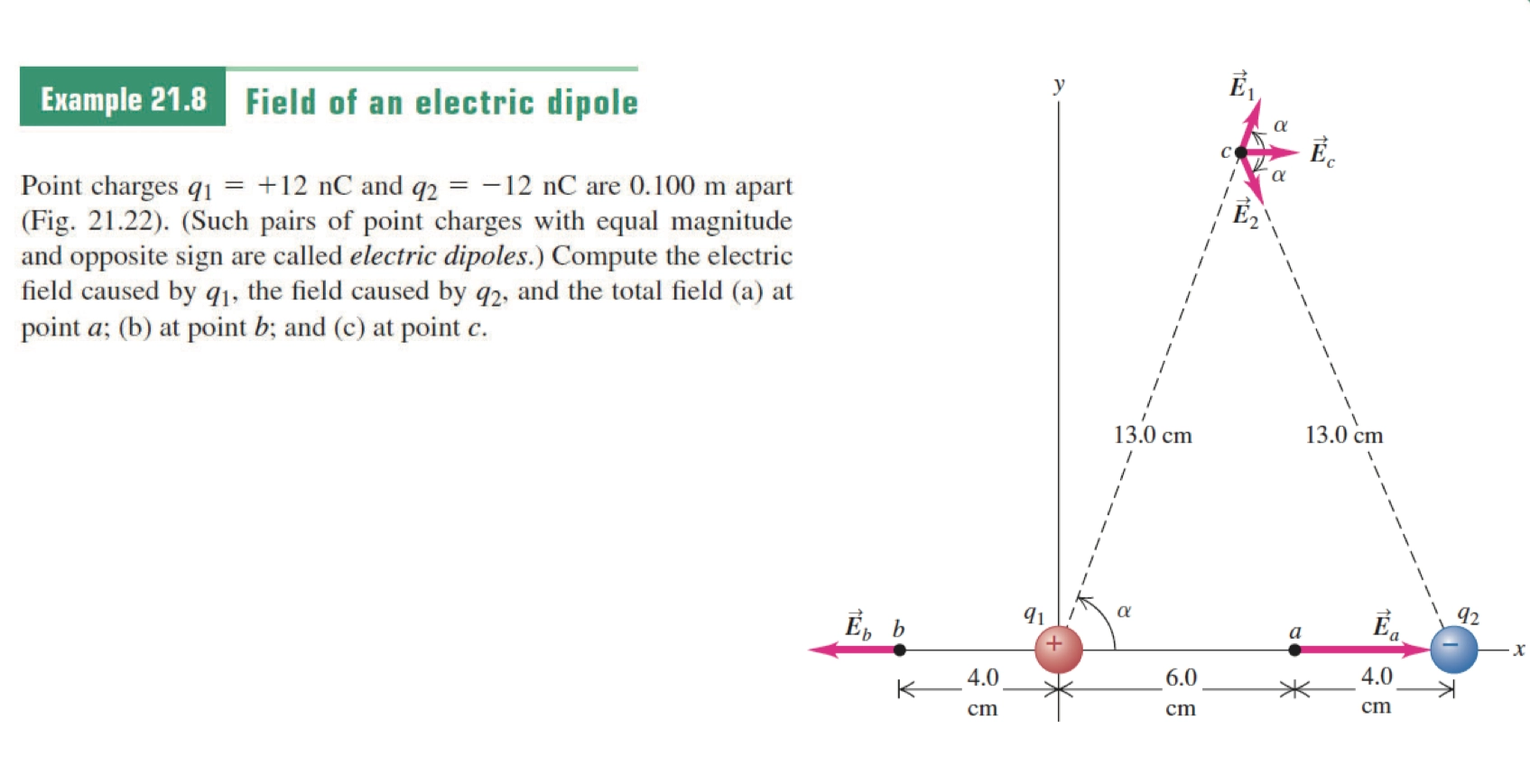
Charged Line Practice 线的电场

• 这个问题有着良好的对称性，所以 P 点在 \(\mathrm{d}E_y\) 上的分量均可以抵消，我们只需要考虑其在 \(\mathrm{d}E_x\) 上的分量，所以

\[ \mathrm{d}E = k\cdot \frac{\mathrm{d}Q}{r^{2}} = \mathrm{d}E_x = k\cdot \frac{\mathrm{d}Q}{r^{2}}\cdot \cos \alpha \]

• 因为这个轴的电荷是均匀分布的，所以 \(\lambda = \frac{Q}{2a}\)

\[ \mathrm{d}Q = \frac{Q}{2a} \cdot \mathrm{d}y \]

• 将其余的变量，\(\alpha , r^{2}\)转换为单一变量

\[ \begin{aligned} \mathrm{d}E_x &= k\cdot \frac{\frac{Q}{2a} \cdot \mathrm{d}y}{(x+y)^{2}}\cdot \frac{x}{\sqrt{x^{2} + y^{2}}} \\ \mathrm{d}E_x &= \frac{Qx}{8\pi \epsilon_0 a} \cdot \frac{dy}{(x^{2}+y^{2})^{\frac{3}{2}}} \end{aligned} \]

• 积分得

\[ \begin{aligned} E = \int \mathrm{d}E_x &= 2 \int_{0}^{a} \frac{Qx}{8\pi \epsilon_0 a} \cdot \frac{\mathrm{d}y}{(x^{2}+y^{2})^{\frac{3}{2}}} ~\mathrm{d}x \\ &= \frac{Qx}{4\pi \epsilon_0 a} \cdot \frac{y}{x^{2}\sqrt{x^{2}+y^{2}}}\bigg|^a_0 \\ &= \frac{Q}{4\pi \epsilon_0 x \sqrt{x^{2}+a^{2}}} \end{aligned} \]

• 当 \(a \to 0\), \(\frac{Q}{4\pi \epsilon_0 x^2}\), 你会发现公式就变成点电荷的公式了

• 当 \(a \to \infty\), \(x^{2} + a^{2} \thickapprox a^{2}\), \(\lambda = \frac{Q}{2a}\)

\[ E = \frac{Q}{4\pi \epsilon_0 x a} = \frac{\lambda}{2\pi \epsilon_0 x} \]

• 你只需要有一些与高斯定律有关的感觉，我们稍后会重新提到这一部分。

Charged Ring Practice 圆环的电场

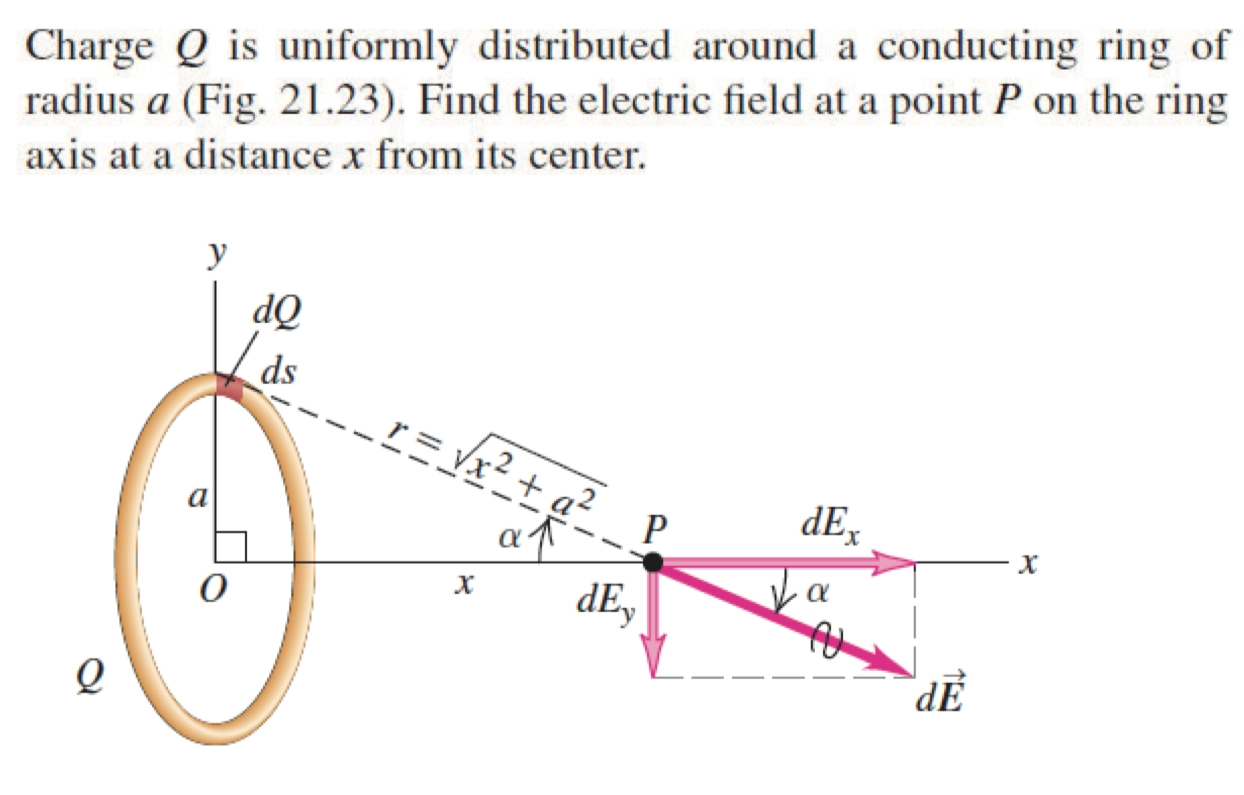
• 同样地，这个问题依然有着良好的对称性，P 点在 \(\mathrm{d}E_y\) 上的分量均可以抵消，我们只需要考虑其在 \(\mathrm{d}E_x\) 上的分量，我们做相似的计算

\[ \mathrm{d}E = k\cdot \frac{\mathrm{d}Q}{r^{2}} = \mathrm{d}E_x = k\cdot \frac{\mathrm{d}Q}{r^{2}}\cdot \cos \alpha = \frac{1}{4\pi \epsilon_0} \cdot \frac{\mathrm{d}Q}{r^{2}}\cdot \frac{x}{r} \]

• 同样地，因为圆环的电荷均匀分布，所以 \(\lambda = \frac{Q}{2\pi a}\)

\[ \mathrm{d}E = \frac{1}{4\pi \epsilon_0} \cdot \frac{\mathrm{d}Q}{r^{2}}\cdot \frac{x}{r} = \frac{1}{4\pi \epsilon_0} \cdot \frac{\frac{Q}{2\pi a}\cdot \mathrm{d}l}{r^{2}}\cdot \frac{x}{r} \]

• 其中 \(x, a, r\) 均为常量，且 \(r = \sqrt{x^{2}+a^{2}}\) 所以我们得到

\[ E = \frac{1}{4\pi \epsilon_0} \cdot \frac{Q}{2\pi a}\cdot\frac{x}{(x^{2}+a^{2})^{\frac{3}{2}}} \int_{0}^{2\pi a} ~\mathrm{d}l = \frac{Q}{4\pi \epsilon_0}\cdot \frac{x}{(x^{2}+a^{2})^{\frac{3}{2}}} \]

• 当 \(x \to 0\), 我们很容易就可以得到 \(E = 0\), 因为所有方向上的电场线都被互相抵消了。
• 当 \(x \to \infty\), 我们也可以得到点电荷的电场式 \(E = \frac{1}{4\pi \epsilon_0}\cdot \frac{Q}{x^{2}}\)

Charged Disk Practice 圆盘的电场

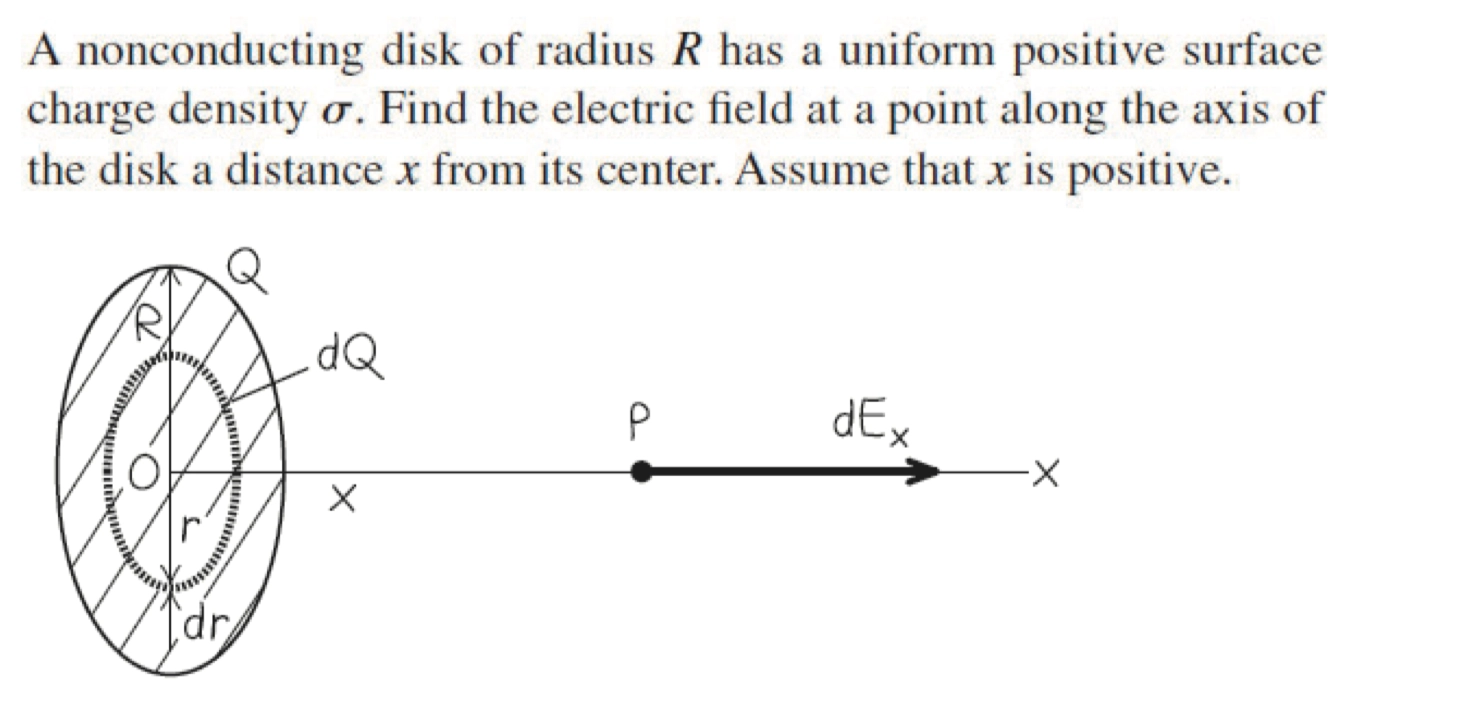
• 首先，我们知道圆环的电场为 \(E = \frac{Q}{4\pi \epsilon_0}\cdot \frac{x}{(x^{2}+a^{2})^{\frac{3}{2}}}\)，所以我们可以将这个圆盘切分成多个圆环，且因为圆盘的电荷密度为 \(\sigma\), 所以我们可以得到 \(\mathrm{d}Q = \sigma \cdot \mathrm{d} A\)，又因为 \(\frac{\mathrm{d}A}{\mathrm{d}r} = (\pi r^{2})' = 2 \pi r\)，所以 \(\mathrm{d}Q = \sigma \cdot \mathrm{d}A = \sigma \cdot 2 \pi r \cdot \mathrm{d}r\)，所以我们有

\[ \mathrm{d}E = \frac{1}{4\pi \epsilon_0}\cdot \frac{x \cdot \mathrm{d}Q}{(x^{2}+r^{2})^{\frac{3}{2}}} = \frac{x \sigma}{4\pi \epsilon_0}\cdot \frac{ 2 \pi r \cdot \mathrm{d}r}{(x^{2}+r^{2})^{\frac{3}{2}}} \]

• 积分得

\[ E = \int \mathrm{d}E = \int_{0}^{R} \frac{x \sigma }{4 \epsilon_0} \cdot \frac{2r \mathrm{d}r}{(x^{2}+r^{2})^{\frac{3}{2}}}~\mathrm{d}x \]

• 使得 \(u = x^{2} + r^{2}\)，得到 \(\frac{\mathrm{d}u}{\mathrm{d}r} = 2r \Leftrightarrow \mathrm{d}r = \frac{\mathrm{d}u}{2r}\)，所以有

\[ \begin{aligned} E &= \int_{0}^{R} \frac{x \sigma }{4 \epsilon_0} \cdot \frac{2r \mathrm{d}r}{(x^{2}+r^{2})^{\frac{3}{2}}}~\mathrm{d}x \\ &= \frac{x \sigma }{4 \epsilon_0} \cdot \int_{0}^{R} \frac{\mathrm{d}u}{u^{\frac{3}{2}}} ~\mathrm{d}u \\ &= \frac{x \sigma }{2 \epsilon_0} \left[ - \frac{1}{\sqrt{x^{2} + R^{2}}} + \frac{1}{x}\right] \\ &= \frac{\sigma}{2 \epsilon_0}\left[ 1 - \frac{1}{\sqrt{(R^{2}/x^{2})+1}} \right] \end{aligned} \]

• 当 \(R \to 0\), 我们可以得到 \(E = \frac{\sigma }{2 \epsilon_0}\)
• 当 \(R \to \infty\), 我们可以得到相同的结果 \(E = \frac{\sigma }{2 \epsilon_0}\)
  • 这也便是后面将会提到的，匀强电场的公式

AP FRQ Practice 真题练习

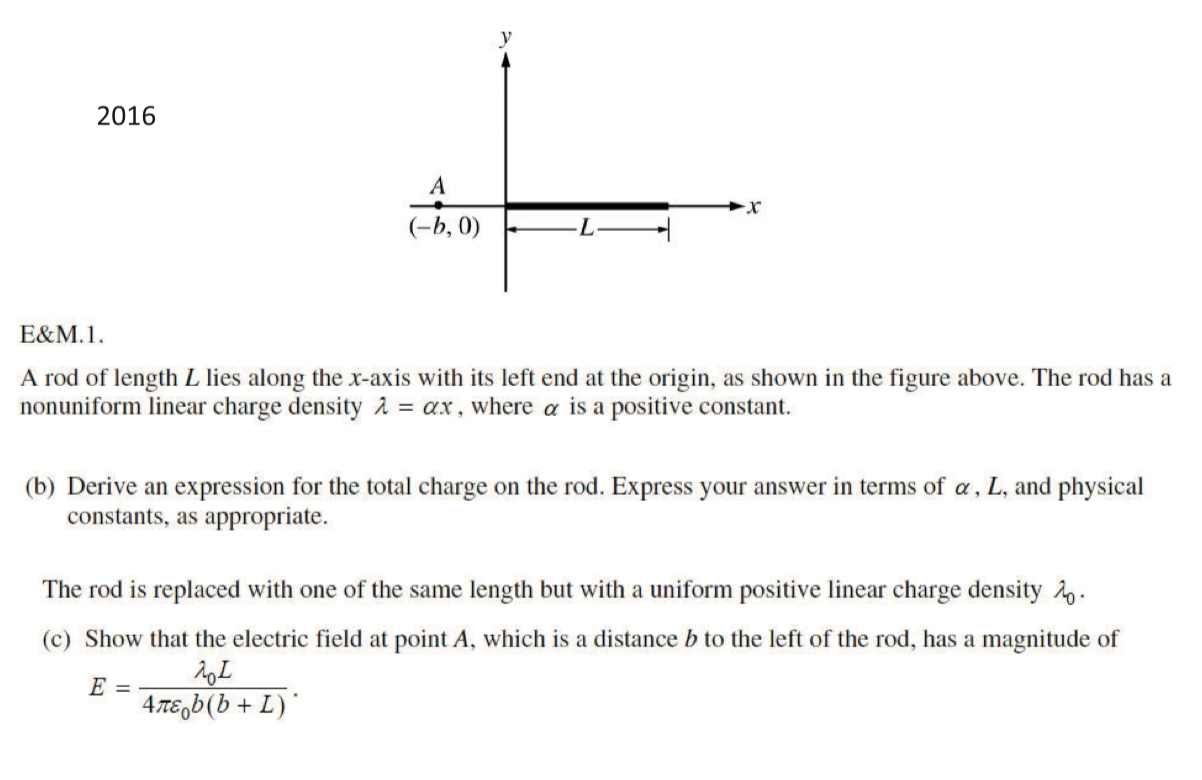
• 我们要求总电荷 \(Q\) 就积电荷的微分 \(\mathrm{d}Q\)，首先确定 \(\mathrm{d}Q\)

\[ \begin{aligned} \mathrm{d}Q &= \lambda \cdot \mathrm{d}x = \alpha x \cdot \mathrm{d}x\\ \int_{0}^{L} ~\mathrm{d}Q &= \int_{0}^{L} \alpha x ~\mathrm{d}x = \frac{1}{2}\alpha L^{2} \end{aligned} \]

• 要求电场就确定 \(\mathrm{d}E\)

\[ \mathrm{d}E = \frac{1}{4 \pi \epsilon_0} \cdot \frac{\lambda_0 \mathrm{d}x}{(x+b)^{2}} \]

• 积分得

\[ \begin{aligned} E &= \frac{\lambda_0}{4\pi \epsilon_0} \int_{0}^{L} \frac{\mathrm{d}x}{(x+b)^{2}} ~\mathrm{d}x \\ &= \frac{\lambda_0L}{4 \pi \epsilon_0 b (b + L)} \end{aligned} \]

• 确定 \(\mathrm{d}Q\)

\[ \mathrm{d}Q = \lambda \cdot \mathrm{d}l = \lambda \cdot R \cdot \mathrm{d} \theta \]

• 可以参照之前的 Semicircle Model Practice 直接得到结果 \(F = \frac{Q \lambda }{2\pi \epsilon_0}\)，得到 \(E = \frac{\lambda }{2\pi \epsilon_0}\)

\[ E = \frac{\lambda}{2\pi \epsilon_0 R} + \frac{\lambda }{2 \pi \epsilon_0 2R} = \frac{3\lambda }{4\pi \epsilon_0 R} \]

Uniform Electric Field 匀强电场

• 当有一个长度为 \(L\) 的平面, \(L \to \infty\), 那么我们可以视这个平面的所产生的电场，是匀强的，称为匀强电场.

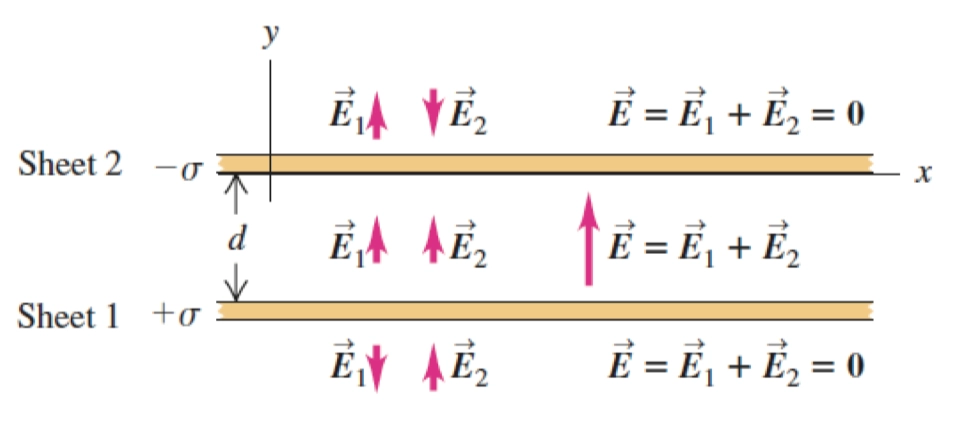
• 在这两款平行板之间的电场便是 \(E = E_1 + E_2 = 2E_1 = 2E_2\)

• AP 2016 C，\(R \gg x\) 所以满足无穷大平面，匀强电场

Electric Potential Energy & Electric Potential 电势能与电势

• 如果一个力是保守力，势能被表示为 \(U\)

\[ W_{a \to b} = \int_{a}^{b} \vec{F} ~ \mathrm{d}\vec{s} = U_a - U_b = -(U_b - U_a) = -\Delta U \]

• 当这个力使得电荷运动时，就有

\[ W_{a \to b} = K_b - K_a = U_a - U_b \Leftrightarrow U_a + K_a = U_b + K_b \]

• 即能量守恒

Electric Potential of Two Points 对比两个不同点的电势能

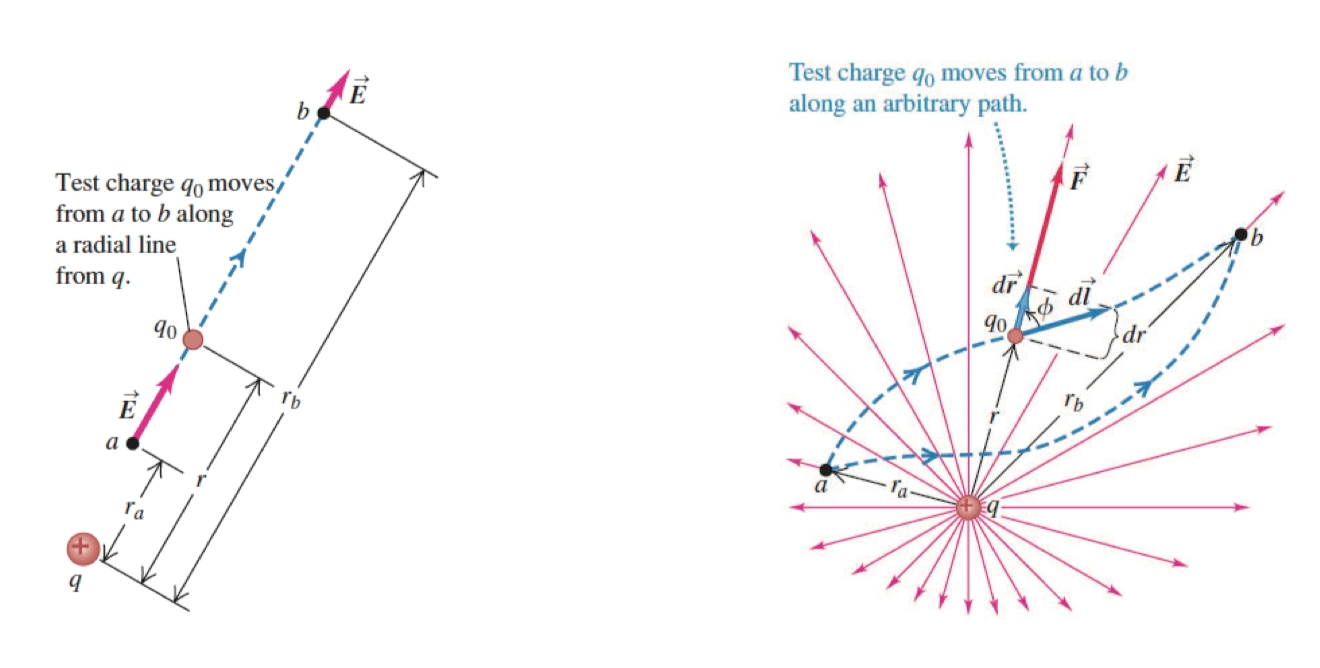
• 乍看上去好像左图和右图完全不一样，其实本质上右图在垂直电场线方向的分量可以完全忽略，也就是相当于如下图所示

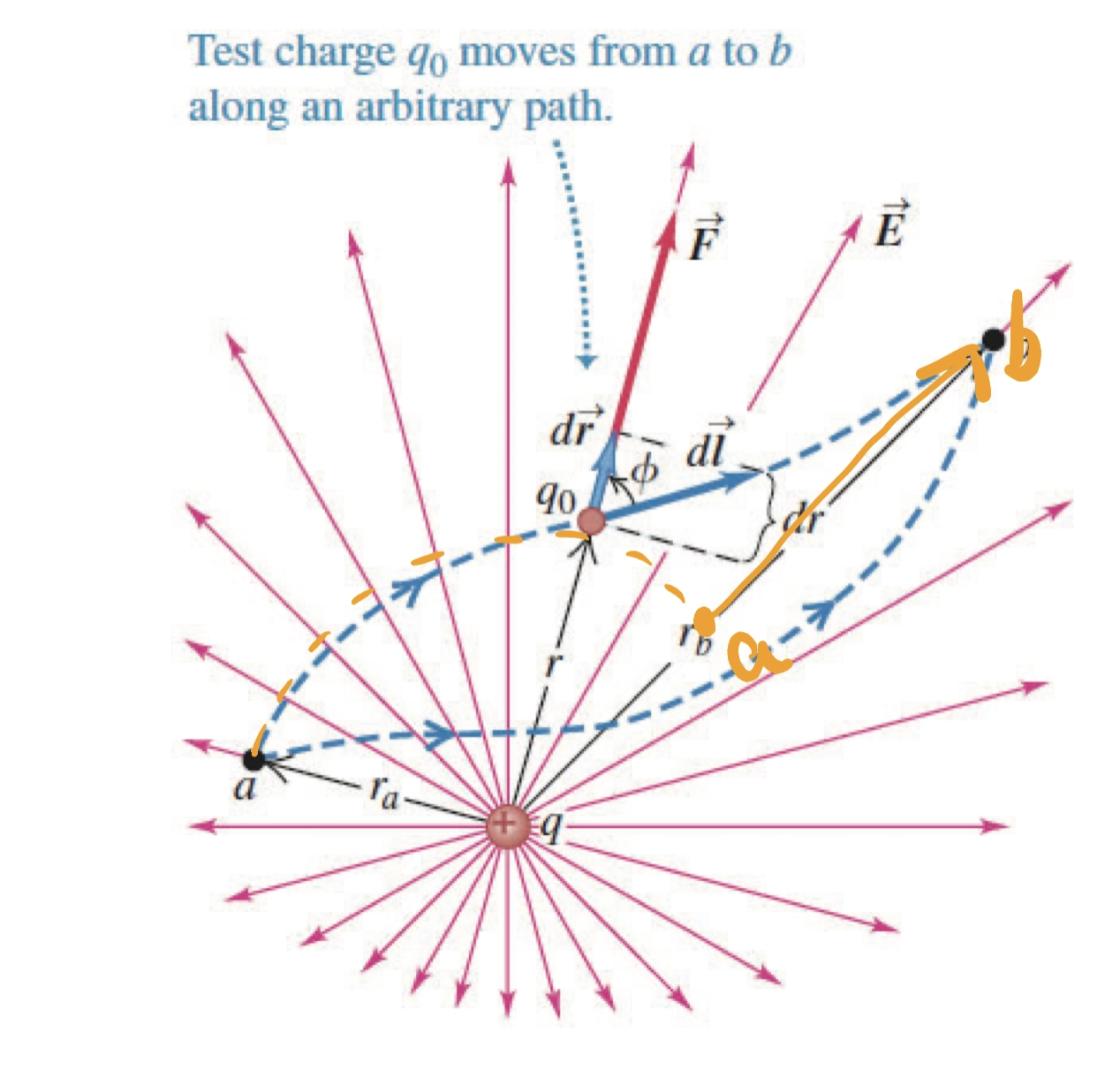
• 由 点 \(a\) （这里 \(a\) 同样代表距离）沿圆线走到另外一个 点 \(a\)，然后直接沿着电场线方向走到点 \(b\)，所以对于上述两个情况的电势，我们都可以写成

\[ \begin{aligned} \Delta U = - W &= - \int F ~ \mathrm{d}r \\ &= -\int_{a}^{b} \frac{1}{4 \pi \epsilon_0} \frac{qq_0}{r^{2}} ~\mathrm{d}r \\ &= \frac{qq_0}{4\pi \epsilon_0} \int_{a}^{b} -\frac{1}{r^{2}} ~\mathrm{d}r \\ &= \frac{qq_0}{4\pi \epsilon_0}\cdot (\frac{1}{b} - \frac{1}{a}) = U_b - U_a \end{aligned} \]

• 而如果我们需要求单个点的电势能，我们首先要确定零点（无穷远处电势能为 \(0\)），可以写成

\[ \begin{aligned} U_b - U_a &= 0 - U_a = \frac{qq_0}{4\pi \epsilon_0}(0 - \frac{1}{a}) \\ U_a &= \frac{qq_0}{4\pi \epsilon_0 a} \end{aligned} \]

• 所以我们可以定义电势能为

\[ \begin{aligned} U &= \frac{1}{4\pi\epsilon_0}\frac{qq_0}{r} = q_0 Er \\ \Delta U &= \frac{qq_0} {4\pi\epsilon_0}\cdot(\frac 1b - \frac 1a) \end{aligned} \]

Electric Potential Energy of Parallel Plates 平行板的电势能

• 由于平行板可以视作无穷大平面，也就是匀强电场，可以得到 \(E = \frac{\sigma}{2 \epsilon_0}\)
• 其中 \(U = q_0 E \Delta x = \frac{\sigma q_0}{2 \epsilon_0} \cdot \Delta x\)

Graph of Electric Potential Energy 电势能的图像

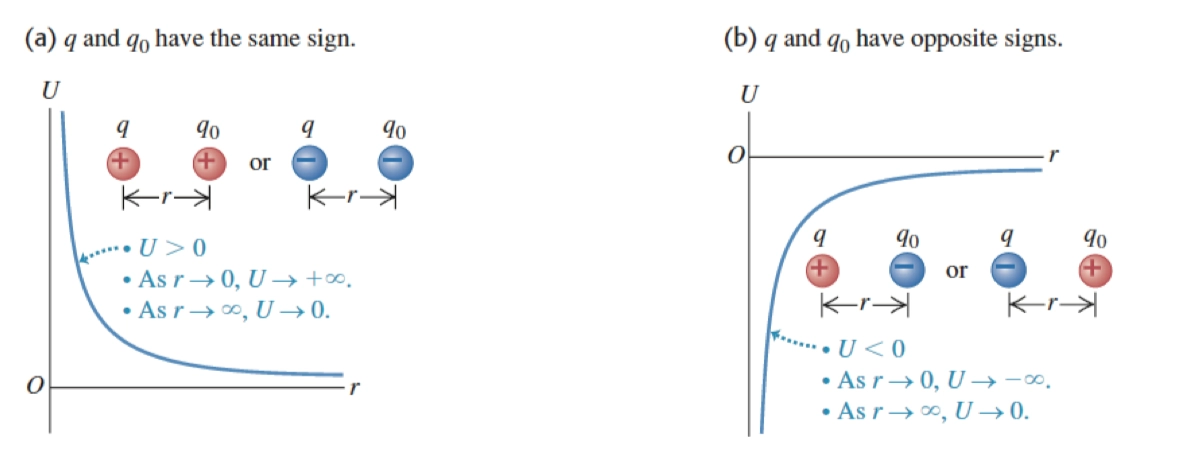
• 如果两个点电荷相同，\(U\) 是正的，如果两个点电荷不相同， \(U\) 是负的
• 而又因为，点电荷之间相同，是斥力，所以力和位移的方向一致，\(U\) 是减少的
• 如果点电荷之间不同，是引力，所以力和位移的方向相反，\(U\) 是增加的

MCQ Practice 练习

• AP 2016: B

• 注意: “work done by external forces” 是指外部力做的功，而非电场力做的功

• AP 2016: B

\[ \begin{aligned} K_0 &= - \Delta U_b = - \frac{qq_0} {4\pi\epsilon_0}\cdot(\frac 1{2d} - \frac 1{d})\\ K_1 &= - \Delta U_b = - \frac{qq_0} {4\pi\epsilon_0}\cdot(\frac 1{4d} - \frac 1{d}) \end{aligned} \]

• 所以我们可以得到 \(K_1 = \frac{3K_0}{2}\)

Electric Potential Energy of Several Point Charges 多个点的电势能

\[ U = \frac{q_0}{4\pi \epsilon}(\frac{q_1}{r_1}+ \frac{q_2}{r_2}+ \frac{q_3}{r_3} + \cdots ) = \frac{q_0}{4\pi \epsilon_0} \sum\limits_{i<j}^{} \frac{q_i q_j}{r_{ij}} \]

• Practice

\[ \begin{aligned} W_{\text{external}} + W_{\text{Electric Field}} = 0 &\Leftrightarrow W_{\text{external}} = - W_{\text{Electric Field}} \\ W_{\text{external}} &= - W_{\text{Electric Field}} \\ &= \Delta U \\ &= \frac{1}{4\pi \epsilon_0}\cdot \left( \frac{q_3q_1}{s}+\frac{q_3q_2}{s} \right) \end{aligned} \]

• AP 2015: A

P 从当前位置到无穷远，同性相斥势能做功，所以 \(K = \frac{kQ^2}{s} + \frac{kQ^2}{s} = \frac{2kQ^2}{s}\)

Electric Potential 电势

• 由于电势总是与测试电荷 \(Q\) 有关，所以我们自然希望得到更普遍的势能形式。因此，这就是电势，意味着每单位电荷的电势 \(U\)

\[ \begin{aligned} V &= \frac{U}{q_0} \quad \text{or} \quad U = q_0 V \\ \pu{1 V} = \pu{1 volt} &= \pu{1 J*C-1} = \pu{1 \text{Joule}*Coulomb-1} \end{aligned} \]

Calculate of Electric Potential 电势的计算

• 电势是电场的属性，与电场一样，与测试电荷没有任何关系

• 点电荷

\[ V = \frac{U}{q_0} = \frac{1}{4 \pi \epsilon_0} \cdot \frac{q}{r} \]

• 电荷若是连续分布

\[ V = \frac{1}{4\pi \epsilon_0} \int \frac{\mathrm{d}q}{r} \]

Property of Electric Potential 电势的性质

• 我们知道功能定理 \(W = -\Delta U\), 所以我们自然地可以得到

\[ W = -q_0 \Delta V \]

• 我们也可以稍微更深入一些，发现他们之间的一些性质

\[ \begin{aligned} W = \int_{a}^{b} \vec{F} \cdot \mathrm{d}\vec{l} = q_0 \int_{a}^{b} \vec{E} \cdot \mathrm{d}\vec{l} &= -q_0\Delta V \\ \int_{a}^{b} \vec{E}\cdot \mathrm{d}\vec{l} &= \int_{a}^{b} E \cos \phi ~ \mathrm{d}l = \int_{a}^{b} E ~\mathrm{d}r = -\Delta V \\ E &= - \frac{\mathrm{d}V}{\mathrm{d}r} \end{aligned} \]

• 电势是一个标量，所以两个电势之和是代数和，而不是矢量和。

Electric Potential of Parallel Plates 平行板的电势

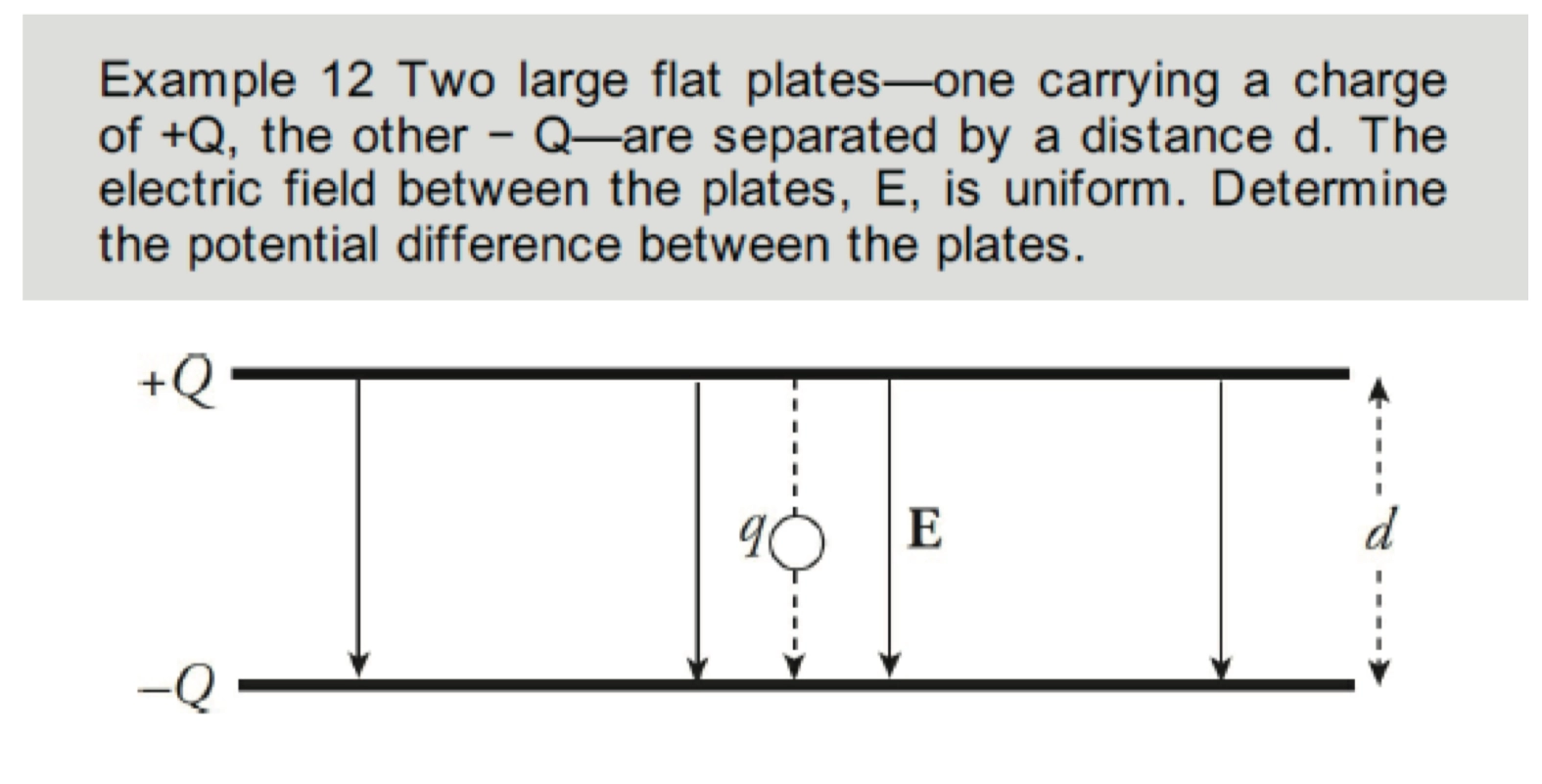
• 我们可以很容易地得到平行板的电动势，即

\[ \left\vert \Delta V \right\vert = \left\vert -\int_{0}^{d} E ~\mathrm{d}r \right\vert = E\cdot d \]

• 因此，我们可以对平行板的电势得出一个一般性的结论，即 \(\left\vert \Delta V \right\vert = E\cdot d\)

Equipotential Surfaces 等势面

• 等势面是一个三维表面，其上每一点的电势 \(V\) 都相同。

• 如果有一个 测试电荷 \(Q\) 在这样的表面上从一点移动到另一点，电势 \(V\) 保持不变，所以电场所做的功 \(W\) 为 \(0\)。

• 电场线与等势面一定是相互垂直的，即 \(\vec{F} \perp \mathrm{d}\vec{s} \perp \vec{E}\)

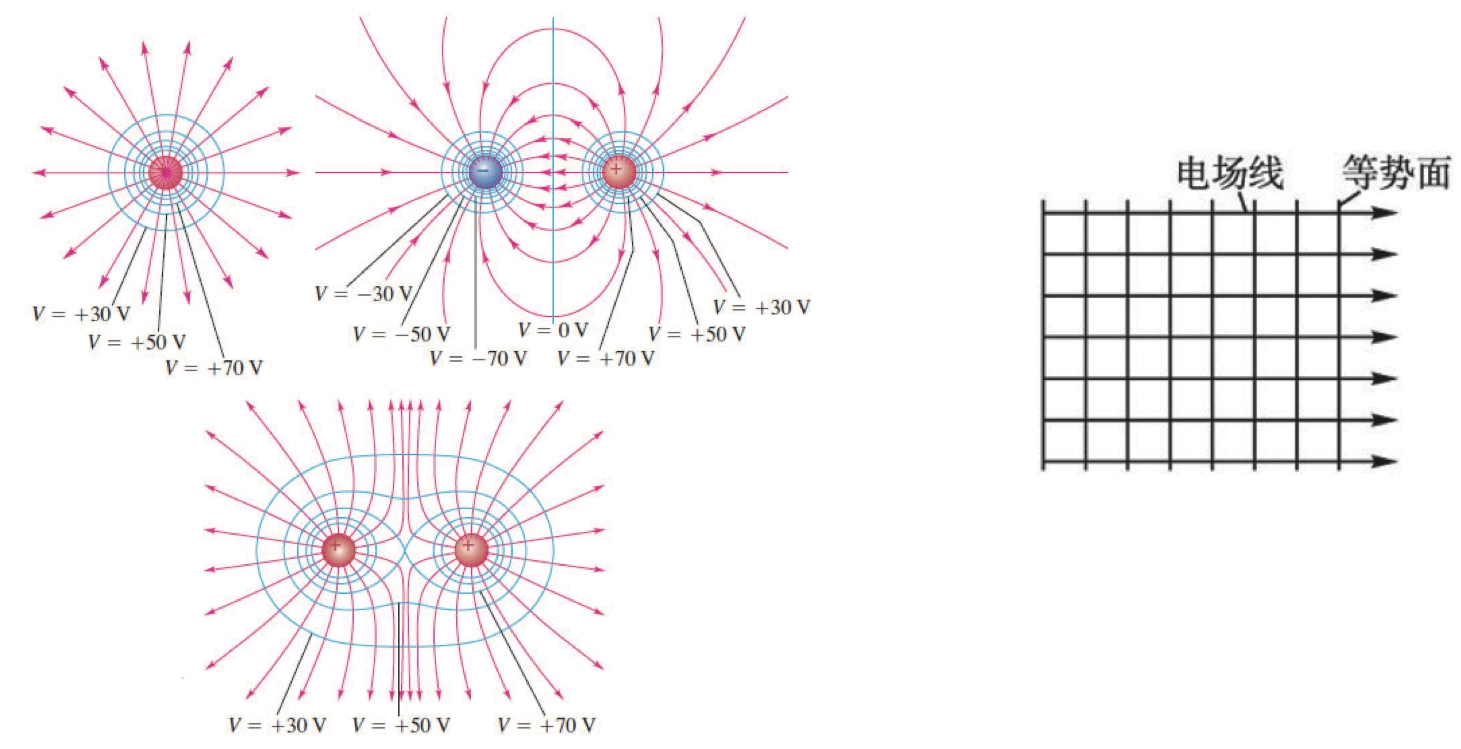
• 所以我们可以观察到 \(E = - \frac{\mathrm{d}V}{\mathrm{d}r}\), 负号 意味着电势随着电场线方向而减少。

MCQ Practice 练习

• AP 2012: B E D

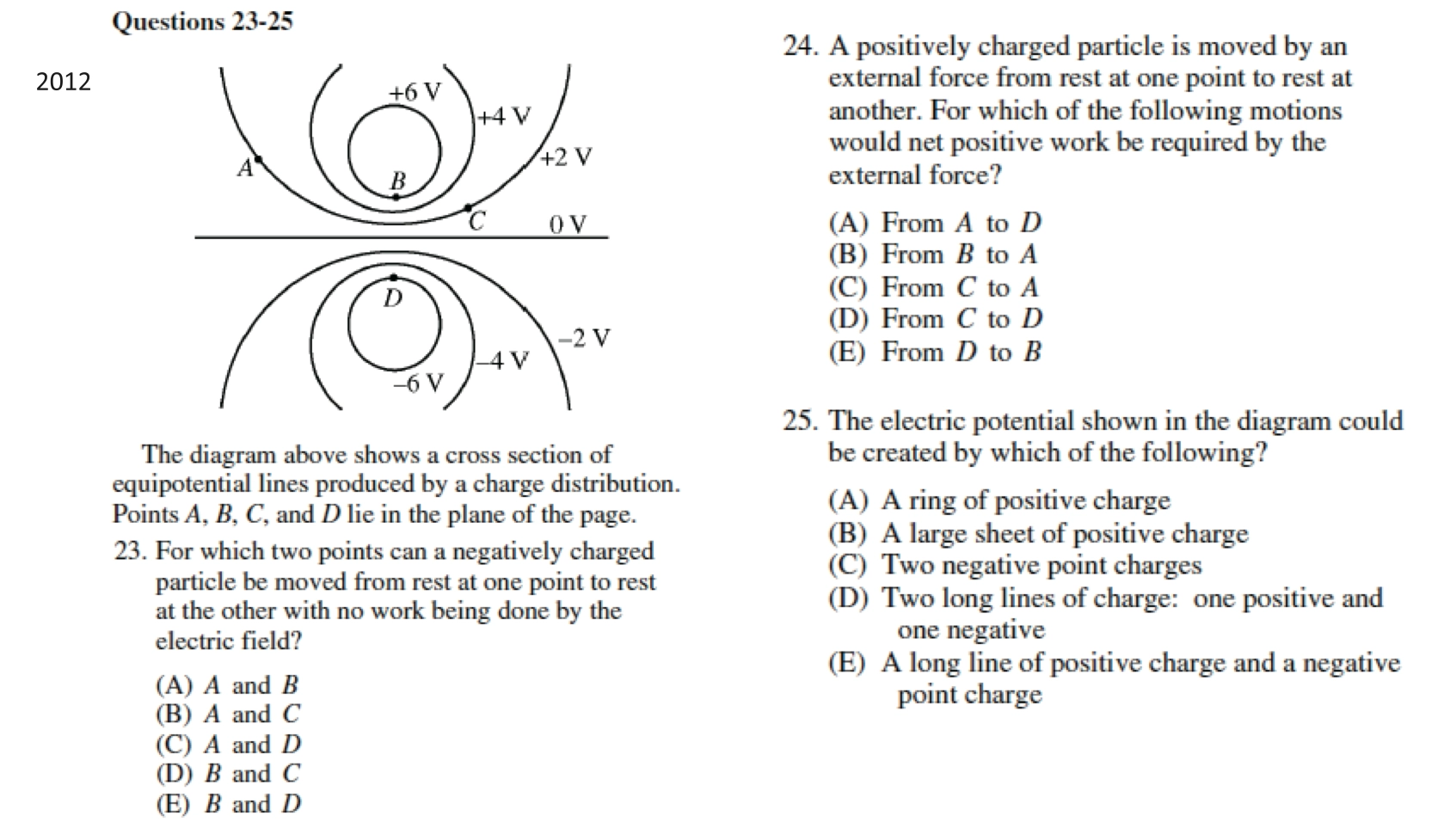
• 同样的是问 “external force”，所以我们需要找到电势增加的方向就是外部力做正功
  • 外部力做正功—增加电势（需要外部的力量克服 \(F_e\) 做功），内部力做正功—减少电势（电势被转化为内部力正功）
• AP 2015: A E

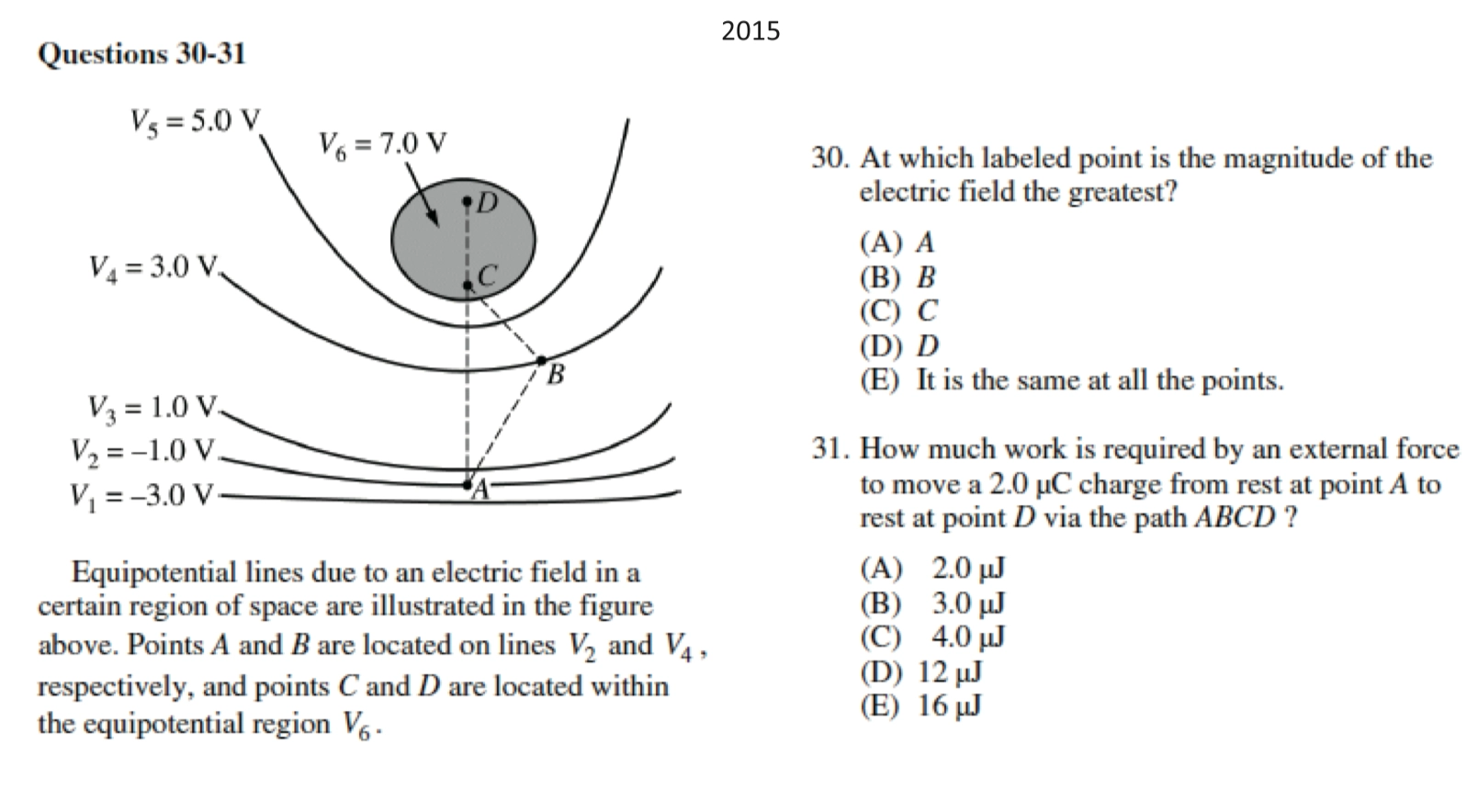
• \(E = - \frac{\mathrm{d}V}{\mathrm{d}r}\) 所以 \(V\) 变化越快，\(E\) 越大

• \(W_{\text{electric field}} = -q_0 \cdot \Delta V = \pu{-2.0 \mu C} \cdot \pu{(7.0 - (- 1.0 )) V} = \pu{16 \mu J}\)

• AP 2016: B

• \(E = - \frac{\mathrm{d}V}{\mathrm{d}r}\) 因为 \(E = 0\)，所以 \(\frac{\mathrm{d}V}{\mathrm{d}r} = 0\)

• 或者说 \(\Delta V = -\int E \mathrm{d}r\) 因为 \(E = 0\)，所以 \(\Delta V = 0\)

Gauss’s Law 高斯定律

• 高斯定律即在一个假象的，封闭的曲面上的电通量满足如下关系

\[ \phi_E = \frac{Q_{\text{enc}}}{\epsilon_0} \]

• 其中，电通量计算如下

\[ \phi_E = \oint \vec{\mathbf{E}} \cdot \mathrm{d}\vec{\mathbf{A}} = \frac{Q_{\text{enc}}}{\epsilon_0} \]

• 通量可以类比为水流以速度 \(\vec{\mathbf{v}}\) 在平面 \(\vec{\mathbf{A}}\) 上的投影于 \(A\) 的乘积，也就是 \(\vec{\mathbf{v}}\) 与 \(\vec{\mathbf{A}}\) 的点积
  • 求流量就是要，先求流过的体积 也就是 \(V = \vec{\mathbf{A}} \cdot \vec{\mathbf{v}} \cdot t\)，但是我们要的是流量，单位时间内的流过的体积，\(V = \frac{\vec{\mathbf{A}} \cdot \vec{\mathbf{v}} \cdot t}{t} = \vec{\mathbf{A}} \cdot \vec{\mathbf{v}}\)

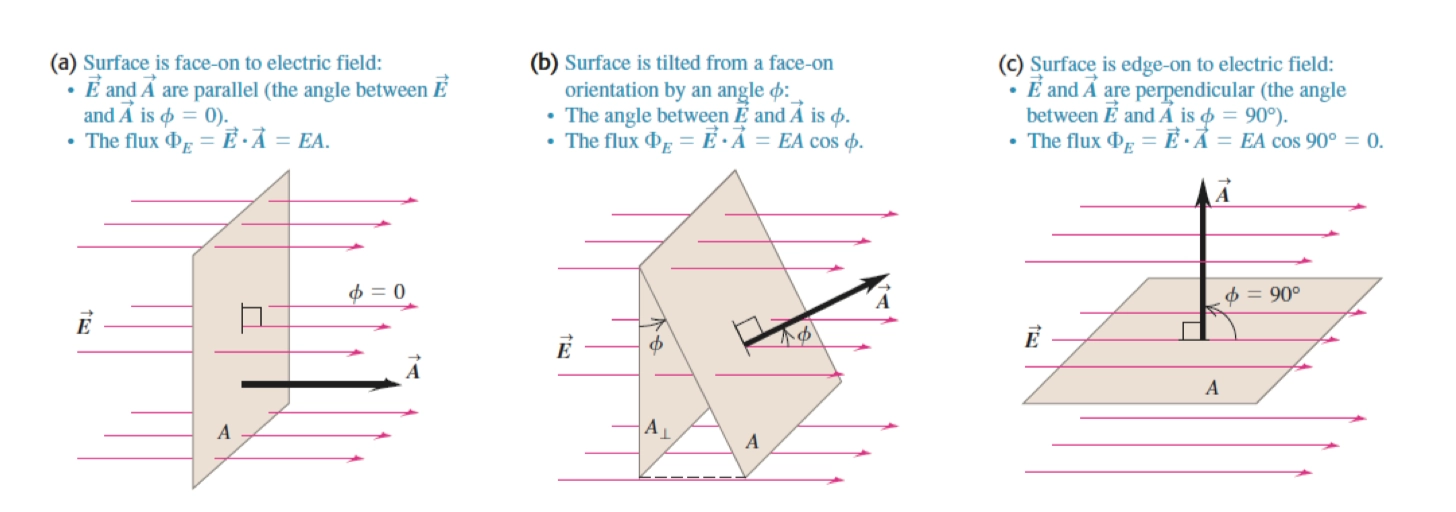
Cube Model Practice 块模型

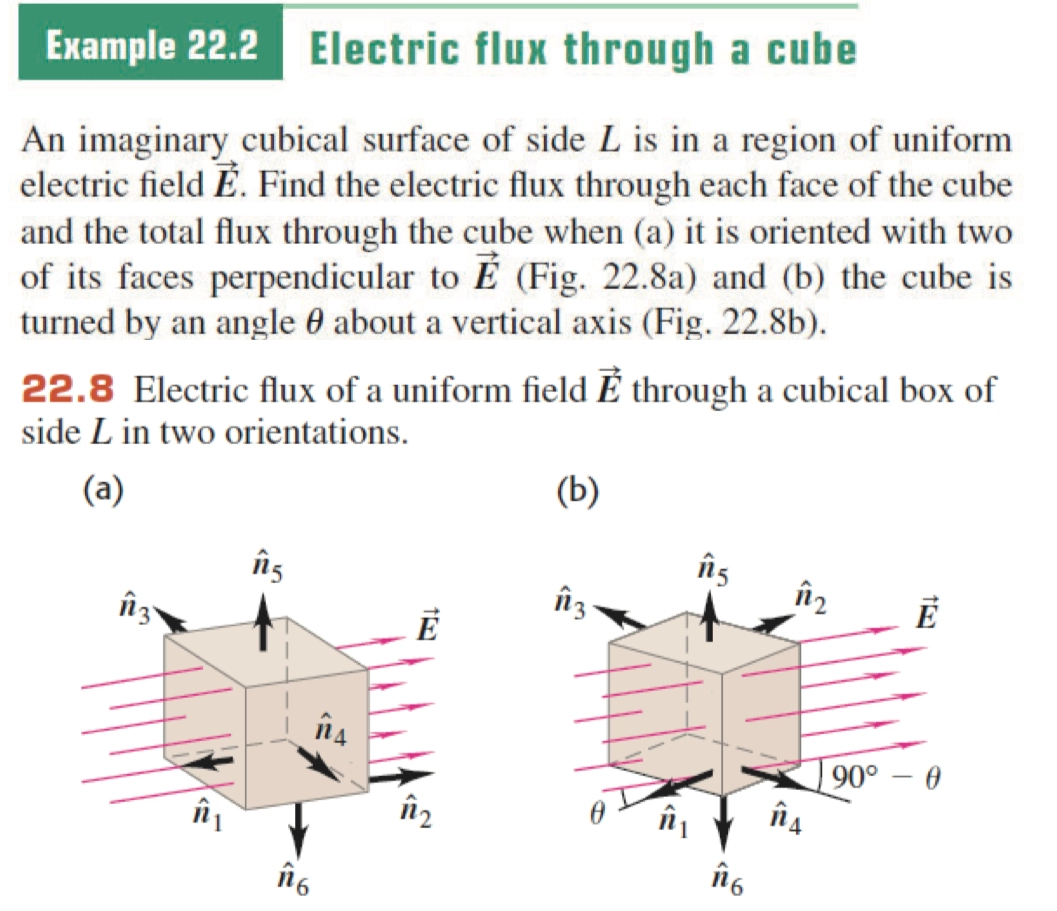
• 无论 a, b 问，对于整体而言，\(\phi _{\text{total}} = 0\)，若单独分析 a 就是 \(A = L^{2}\)，b 就是 \(A = L^{2} \cdot \cos (90^{\circ} - \theta )\)

Simple Point Charge Model 简单点电荷模型

• 定义单位向量方向为 \(\hat{r}\)，对于圆球而言，有良好的几何性质，对于所有的 \(\hat{r}\) 都有 \(\hat{r} \perp \vec{\mathbf{A}}\)
• 其中，圆球的表面积为 \(A = 4\pi r^{2}\)，另附 \(V = \frac{4}{3}\pi r^{3}\)

\[ \begin{aligned} \phi_E &= \oint \vec{\mathbf{E}} \cdot \mathrm{d}\vec{\mathbf{A}} \\ &= \oint \frac{1}{4\pi \epsilon_0} \frac{q}{r^{2}}\cdot \hat{r}\cdot \mathrm{d}\vec{\mathbf{A}} \\ &= \frac{1}{4\pi \epsilon_0}\cdot \frac{q}{r^{2}} \oint \mathrm{d}A \\ &= \frac{1}{4\pi \epsilon_0}\cdot \frac{q}{r^{2}} \cdot 4\pi r^{2} \\ &= \frac{q}{\epsilon_0} \end{aligned} \]

• 我们可以观察到，这个结果与高斯定律不约而同 \(\phi_E = \frac{Q_{\text{enc}}}{\epsilon_0}\)

Gaussian Surface 高斯面

• 高斯面是假象地，且封闭地曲面

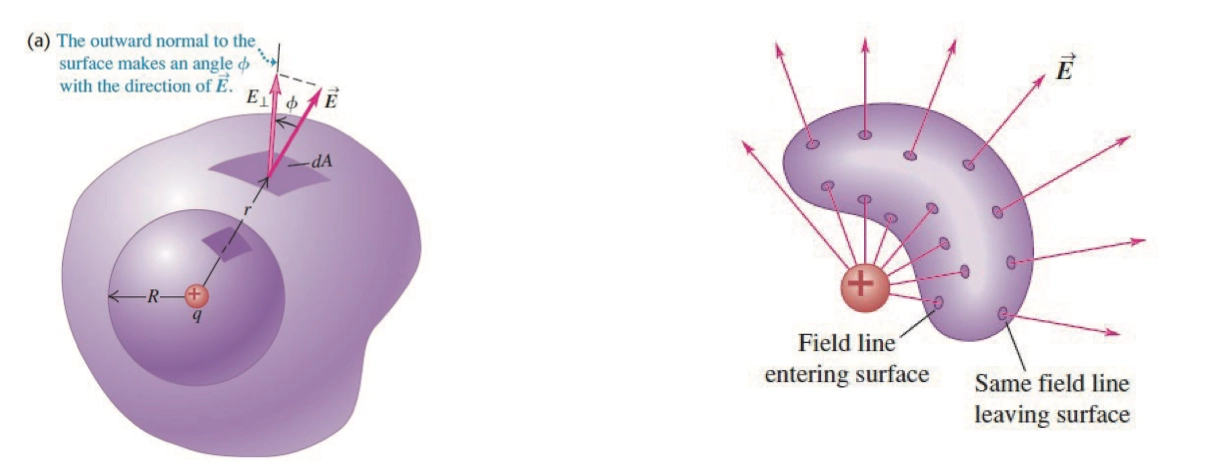
• 如 a，你可以选非常复杂的曲面和简单的球面，结果都是一样的
• 但如果选取的假象面没有包裹点电荷，那么所包裹的电荷就是 \(0\)，电通量也会是 \(0\)

How to Choose Gaussian Surface 如何选择高斯面

• 最好为对称的，电场上处处相等，电场与面垂直或者平行

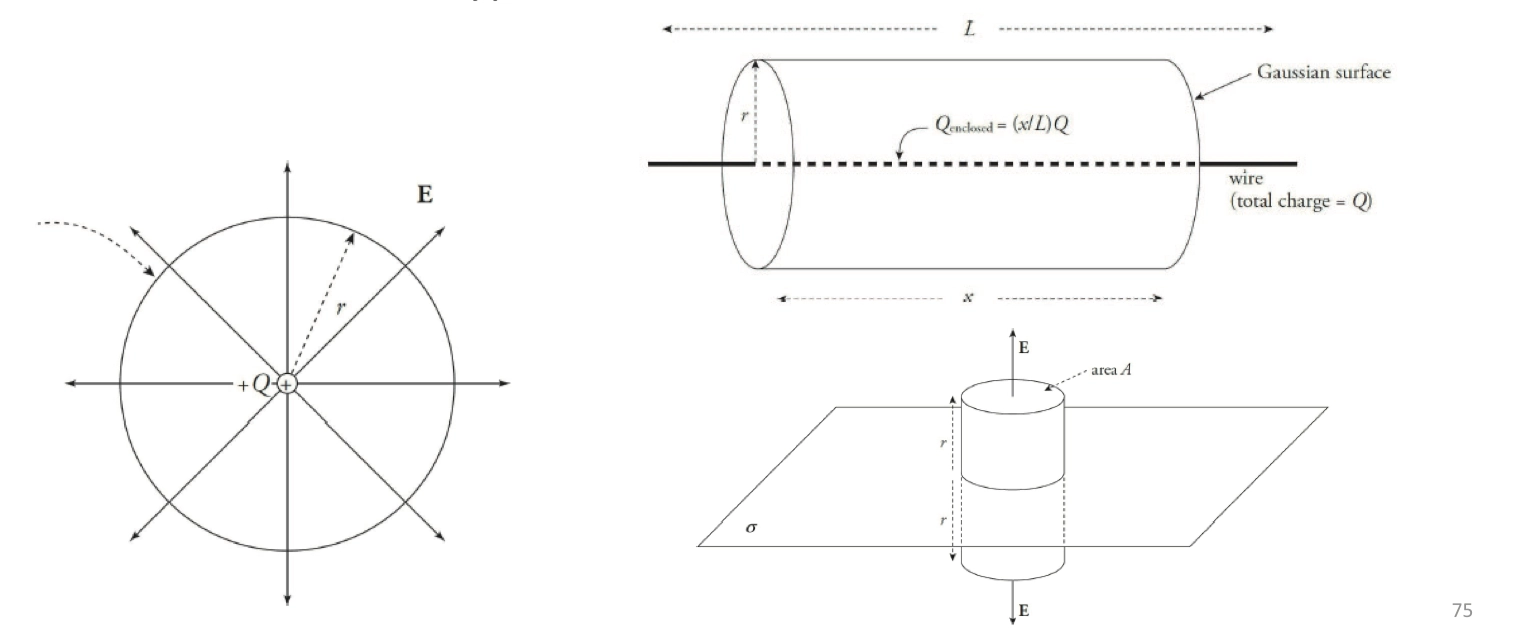
• AP 考试脱离不了这三种简单模型
  • 同心球面，适用于 球形对称的电荷分布
  • 圆柱壳，适用于 长直导线，有中心轴，绕中心轴不变的电荷分布
  • 被平面平分的圆柱，适用于 （有厚度的）无限大平面（ $$ 是常量 ）

Improved Simple Point Charge Model 点电荷模型

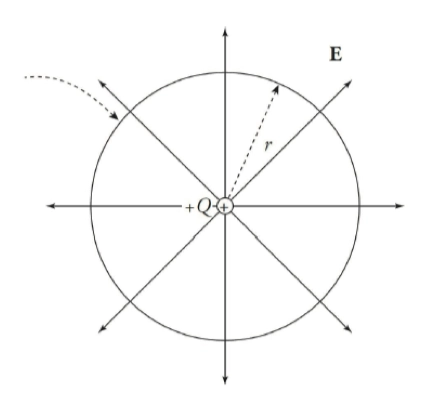
• 首先对于点电荷 \(+Q\) 我们构造同心球面的假象高斯面，由于 \(E = k\cdot \frac{q}{r^{2}}\) 只与 \(r\) 有关，所以我们可以将高斯面上的任意一点 \(E\) 认为是恒定且相等的。

\[ \begin{aligned} \phi_E &= \oint \vec{\mathbf{E}} \cdot \mathrm{d}\vec{\mathbf{A}} = \frac{Q_{\text{enc}}}{\epsilon_0} \\ &= E \cdot \oint \mathrm{d}A \\ &= E \cdot 4\pi r^{2} = \frac{Q_{\text{enc}}}{\epsilon_0} \end{aligned} \]

• 所以我们可以得到 \(E = \frac{Q_{\text{enc}}}{4\pi r^{2}\epsilon_0}\)

MCQ Practice 练习

• AP: C A

• 显然地，无论用 A 还是 B 包裹 \(+q\)，\(Q_{\text{enc}}\) 始终是不会变化的

• AP 2016: A

• 显然地，Q 的电场线将进入圆柱又从圆柱中出来，总和为 \(0\)

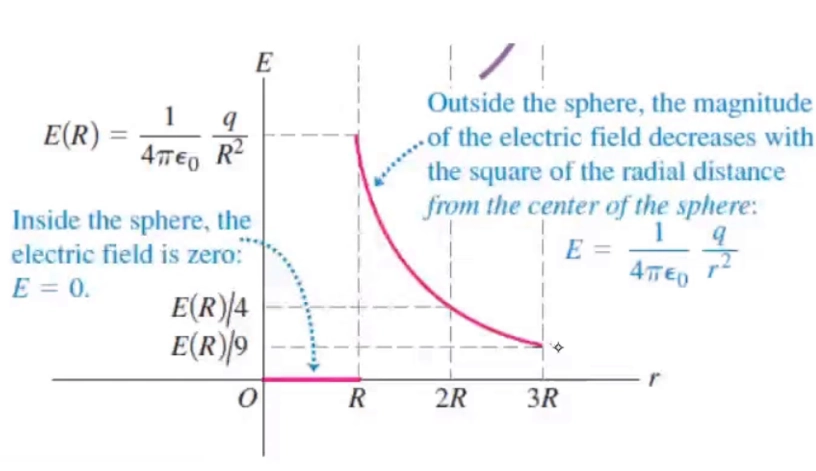
Conducted Sphere Model 导体圆球模型

• 首先，导体意味着电荷都将分布在边缘，也就是中心没有任何电荷

• 所以在球内 \(E = 0\)

• 对于球外

\[ \begin{aligned} \phi_E &= \oint \vec{\mathbf{E}} \cdot \mathrm{d}\vec{\mathbf{A}} = \frac{Q_{\text{enc}}}{\epsilon_0} \\ &= E\cdot 4 \pi r^{2} = \frac{Q_{\text{enc}}}{\epsilon_0} = \frac{q}{\epsilon_0} \end{aligned} \]

• 所以 \(E = \frac{1}{4 \pi \epsilon_0}\cdot \frac{q}{r^{2}}\)，与点电荷一致

• 其关系也可以由下图观察

Improved Sphere Model 复杂圆球模型

• 首先我们发现电荷并不是均匀分布，但是仍然沿着径向分布，也就是说同一个球面上的 $$ 是一致的，且球面上点的电磁学性质也是等价的
• 对于球内，我们选取半径为 \(R\) 的高斯面

\[ \begin{aligned} \phi_E &= \oint \vec{\mathbf{E}} \cdot \mathrm{d}\vec{\mathbf{A}} = E \cdot \oint \mathrm{d}A = \frac{Q_{\text{enc}}}{\epsilon_0} \\ &= E \cdot 4\pi R^{2} = \frac{Q_{\text{enc}}}{\epsilon_0} \\ \end{aligned} \]

• 对于 \(Q_{\text{enc}}\) 我们有

\[ \begin{aligned} Q_{\text{enc}} &= \int_{0}^{R} \rho_0(\frac{r}{a})^{2} \cdot 4\pi r^{2} ~\mathrm{d}r \\ &= \frac{4\pi \rho_0}{a^{2}}\cdot \frac{R^{5}}{5} = \frac{4\pi R^{5} \rho_0}{5a^{2}} \\ \end{aligned} \]

• 所以对于 \(E\) 我们有

\[ E \cdot 4\pi R^{2} = \frac{4\pi R^{5} \rho_0}{5a^{2}\epsilon_0} \Leftrightarrow E = \frac{\rho_0 R^{3}}{5a^{2}\epsilon_0} \]

• 同样地对于球外，我们选取半径为 \(r\) 的高斯面

\[ \begin{aligned} Q_{\text{enc}} &= \int_{0}^{a} \rho_0(\frac{r}{a})^{2} \cdot 4\pi r^{2} ~\mathrm{d}r \\ &= \frac{4\pi \rho_0}{a^{2}}\cdot \frac{a^{5}}{5} = \frac{4\pi a^{5} \rho_0}{5a^{2}} = \frac{4\pi a^{3} \rho_0}{5} \\ \end{aligned} \]

• 所以对于 \(E\) 我们有

\[ E \cdot 4\pi r^{2} = \frac{4\pi a^{3} \rho_0}{5 \epsilon_0} \Leftrightarrow E = \frac{\rho_0 a^{3}}{5\epsilon_0 r^{2}} \]

Electric Potential of Sphere Model 复杂球模型的电势

Long Line Model 无限长直导线模型

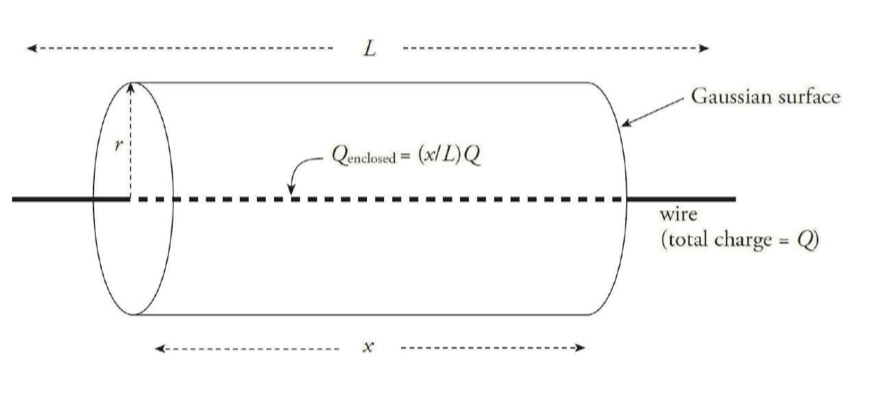
• 首先，构造高斯面，选取了半径为 \(r\) 的圆柱体，以图示方式放置，由于是无限长直导线，我们可以将每个方向上的电场看作是匀强电场，如下图所示

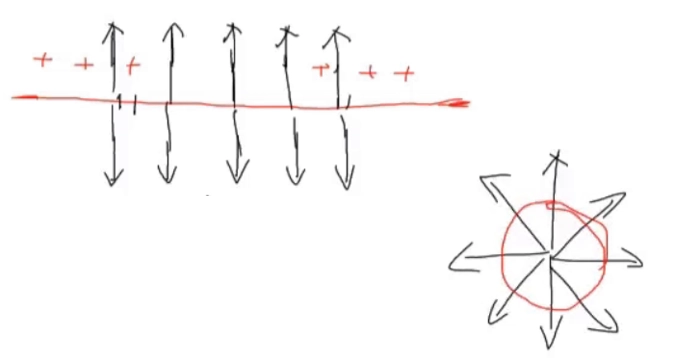
• 而左右两个面方向上显然是没有电通量的，所以我们不考虑，便直接计算圆柱面上的电通量
• 圆柱面上的匀强电场有很良好的性质，都是大小相等的

\[ \begin{aligned} \phi_E &= \oint \vec{\mathbf{E}} \cdot \mathrm{d}\vec{\mathbf{A}} = E \cdot \oint \mathrm{d}A = \frac{Q_{\text{enc}}}{\epsilon_0} \\ &= E \cdot 2\pi x = \frac{Q_{\text{enc}}}{\epsilon_0} \\ \end{aligned} \]

• 对于 \(Q_{\text{enc}}\) 我们有

\[ \begin{aligned} Q_{\text{enc}} &= x \cdot \frac{Q}{L} \end{aligned} \]

• 所以对于 \(E\) 我们有

\[ E = \frac{Q/L}{2\pi \epsilon_0 r} = \frac{\lambda }{2\pi \epsilon_0 r} \]

Electric Potential of Long Line Model 无限长直导线模型的电势

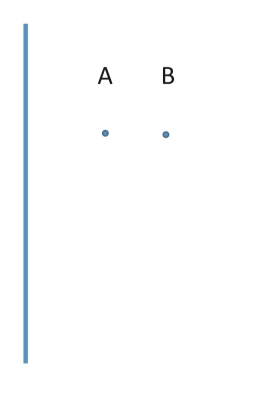
• 若要计算电势，考虑上图 a, b 两点的电势差，我们知道 $V_{ab} = -_{a}^{b} E ~r $

\[ \Delta V_{ab} = -\int_{a}^{b} E ~\mathrm{d}r = -\int_{a}^{b} \frac{1}{2\pi \epsilon_0} \cdot \frac{\lambda }{r} ~\mathrm{d}r = \frac{\lambda }{2\pi \epsilon_0} \ln \frac{a}{b} \]

(注: 这里将负号转化为了 $$ 对数内的 \(\frac{b}{a}^{-1}\) 次方 也就是 \(\frac{a}{b}\))

• 则有 \(\Delta V_{ab} = \frac{\lambda}{2\pi\epsilon_0} \ln \frac ab\), \(V = \frac{\lambda}{2\pi\epsilon_0}\ln \frac{L+d}{d}\)

Plate Model 无穷大平面模型

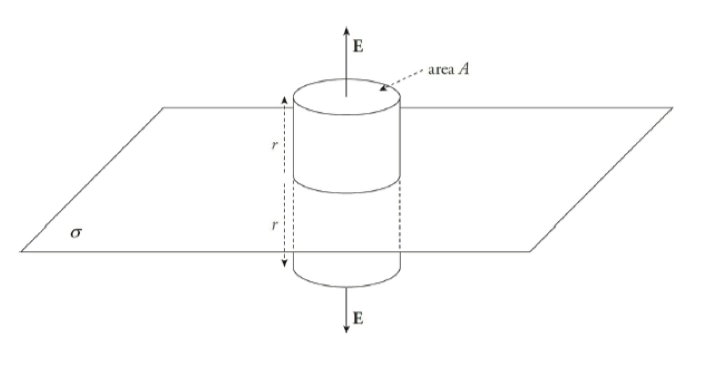
• 首先，构造高斯面，以如图所示的方式构造半径为 \(r\) 的圆柱，我们可以将上下两个方向的电场看作是匀强电场
• 所以只有上下两个面需要考虑，圆柱面的电通量为 \(0\) 不需要考虑
• 由于是匀强电场，同样具有很良好的性质，都是大小相等的

\[ \begin{aligned} \phi_E &= \oint \vec{\mathbf{E}} \cdot \mathrm{d}\vec{\mathbf{A}} = 2E \cdot \oint \mathrm{d}A = \frac{Q_{\text{enc}}}{\epsilon_0} \\ &= 2E \cdot \pi r^{2} = \frac{Q_{\text{enc}}}{\epsilon_0} \\ \end{aligned} \]

• 对于 \(Q_{\text{enc}}\) 我们有

\[ Q_{\text{enc}} = \pi r^{2} \sigma \]

• 所以对于 \(E\) 我们有

\[ E = \frac{\pi r^{2} \sigma}{2\pi r^{2} \epsilon_0 } = \frac{\sigma }{2\epsilon_0 } \]

• 对于无穷大平面模型的电势 已经在 Electric Potential of Parallel Plates 讨论，不重复赘述

Charged Ring Model 圆环模型

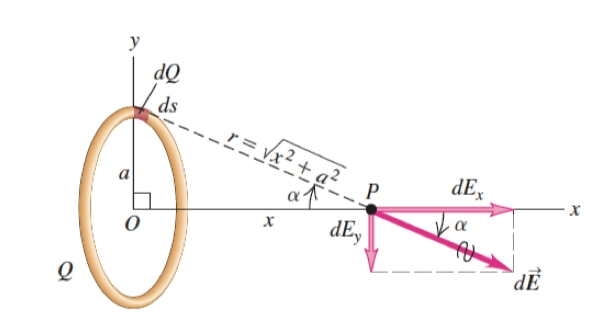
• 对于已经讨论过的 Charged Ring Practice，我们知道 \(E = \frac{Q}{4\pi \epsilon_0}\cdot \frac{x}{(x^{2}+a^{2})^{\frac{3}{2}}}\)，若使用电场直接积分，过程会十分曲折复杂

• 所以我们考虑其 \(x_1 \to x_2\) 的电势差 \(\Delta V\)，通过对点电荷电势进行积分

\[ \begin{aligned} \mathrm{d}V &= \frac{1}{4\pi \epsilon_0}\cdot \frac{\mathrm{d}Q}{r} \\ ~ \\ V &= \int \mathrm{d}V = \frac{1}{4\pi \epsilon_0 \cdot r} \cdot \int \mathrm{d}Q = \frac{Q}{4 \pi \epsilon_0} \cdot \frac{1}{\sqrt{x^{2} + a^{2}}} \end{aligned} \]

• 自然地，\(\Delta V\) 可以求得

\[ \Delta V = kQ(\frac{1}{\sqrt{x_2^2 +a^2}} - \frac{1}{\sqrt{x_1^2+a^2}}) \]

AP FRQ Practice 练习

\[ \begin{aligned} Q &= \int_{a}^{2a} \rho ~\mathrm{d}V = \int_{a}^{2a} br^{2}\cdot 4\pi r^{2} ~\mathrm{d}r \\ &= 4 \pi b \cdot \frac{r^{5}}{5} \bigg|^{2a}_{a} = \frac{124 \pi b a^{5}}{5} \end{aligned} \]

• \(r > 2a\)

\[ \begin{aligned} E \cdot 4\pi r^{2} &= \frac{Q_{\text{enc}}}{\epsilon_0} = \frac{124 \pi b a^{5}}{5} \\ E &= \frac{31 b a^{5}}{5r^{2} \epsilon_0} \end{aligned} \]

• \(r < a\)，高斯面内无电荷，\(E = 0\)

• \(r < R\)

\[ E \cdot 2 \pi r x = \frac{Q_{\text{enc}}}{\epsilon_0} = \frac{\rho \pi r^{2} x }{\epsilon_0} E = \frac{\rho r}{2 \epsilon_0} \]

• \(r > R\)

\[ E \cdot 2\pi rx = \frac{Q_{\text{enc}}}{\epsilon_0} = \frac{\rho \pi R^{2} x }{\epsilon_0} E = \frac{\rho R^{2}}{2 r \epsilon_0} \]

AP MCQ Practice MCQ 练习

• AP 2013: A

• \(E = \frac{\lambda}{2\pi \epsilon_0 r}\), 所以 \(E \propto \frac{1}{r}\)

• AP 2013: E

• 通过圆环的电势公式可知 \(V = kQ(\frac{1}{\sqrt{x_2^2 +a^2}} - \frac{1}{\sqrt{x_1^2+a^2}})\)

总结

• \(\Delta U = \frac{qq_0}{4\pi\epsilon_0}\cdot(\frac 1b - \frac 1a)\)

• \(W = -q_0 \Delta V\)

• \(E = - \frac{\mathrm{d}V}{\mathrm{d}r}\)

• \(\phi_E = \oint \vec{\mathbf{E}} \cdot \mathrm{d}\vec{\mathbf{A}} = \frac{Q_{\text{enc}}}{\epsilon_0}\)

• 半圆模型

  • \(E = \frac{\lambda }{2\pi \epsilon_0}\)

• 线模型

  • \(E = \frac{Q}{4\pi \epsilon_0 x \sqrt{x^{2}+a^{2}}}\)

• 圆环

  • \(E = \frac{kQx}{(x^2+a^2)^{\frac 32}}\), \(\Delta V = kQ(\frac{1}{\sqrt{x_2^2 +a^2}} - \frac{1}{\sqrt{x_1^2+a^2}})\)

• 圆盘

  • \(E = \frac{x \sigma }{2 \epsilon_0} \left[ - \frac{1}{\sqrt{x^{2} + R^{2}}} + \frac{1}{x}\right] = \frac{\sigma}{2 \epsilon_0}\left[ 1 - \frac{1}{\sqrt{(R^{2}/x^{2})+1}} \right]\)

• 圆球

  • \(V = \frac 34\pi r^3\), \(\mathrm{d}V = 4\pi r^2 \mathrm{d} r\)
  • \(E_{\text{inner}} = \frac{kQr}{R^3}\) （非导体） \(E_{\text{outer}} = \frac{kQ}{r^2}\)
  • \(V_{\text{inner}} = kQ\frac{3R^2-r^2}{2R^3}\), \(V_{\text{outer}} = kQ (\frac 1{r_a} - \frac 1{r_b})\)
  • \(C = \frac{\epsilon_0 \cdot 4\pi r_a r_b}{r_b - r_a}\)

• 空心圆球

  • \(V = \frac 34\pi (R^3-r^3)\), \(\mathrm{d} V = 4\pi r^2 \mathrm{d} r\) （与圆球一致）
  • \(E_{\text{inner}} = 0\) \(E_{\text{outer}} = \frac{kQ}{r^2}\)（匀质）

• 无穷长直导线

  • \(E = \frac{Q/L}{2\pi r \epsilon_0} = \frac{\lambda}{2\pi r \epsilon_0}\), \(\Delta V = \frac{\lambda}{2\pi\epsilon_0} \ln \frac ab\), \(V = \frac{\lambda}{2\pi\epsilon_0}\ln \frac{L+d}{d}\)
  • \(C= \frac{2\pi\epsilon_0}{\ln \frac{r_b}{r_a}}\)

• 无穷大平面（匀强电场）

  • \(E = \frac{\sigma}{2\epsilon_0}\) ，\(\left\vert \Delta V \right\vert = E\cdot d\)

• 平行板电容器

  • \(E = \frac{Q}{\epsilon_0A}\), \(V = \frac{Qd}{\epsilon_0A}\), \(\left\vert \Delta V \right\vert = E\cdot d\)
  • \(C = \epsilon_0\frac{A}{d}\)