本笔记直接从 Notion 签出，格式混乱，内容或有错误，仅供参考

微分方程 Differential Equation

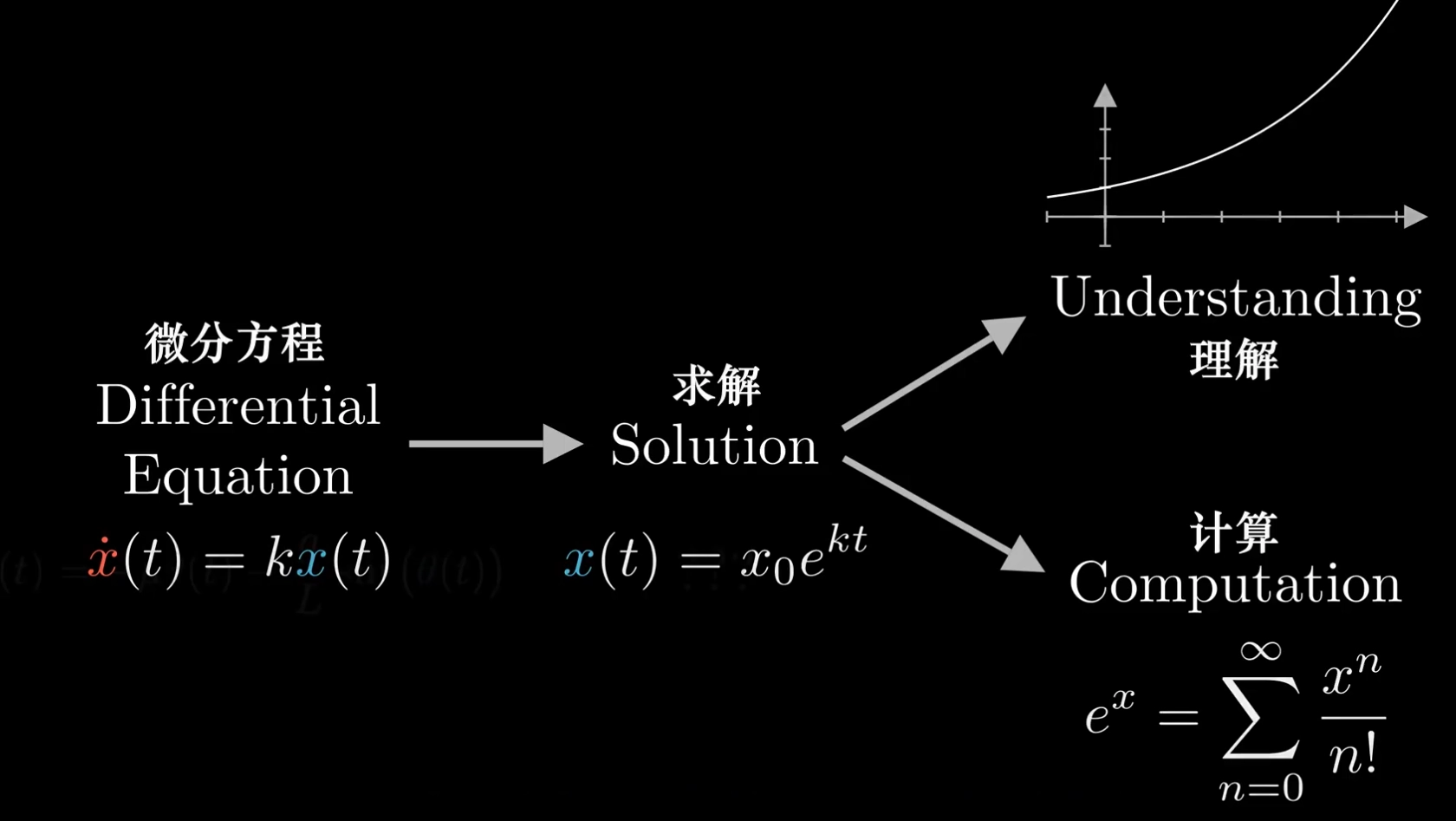
为何使用 DE

• 当描述相对变化量（\(\Delta x\)）比绝对量（\(x\)）更简单时，DE就会被经常用到了。
• 显然的，导数相较于原函数是更简单更加容易研究的一种存在。导数也就是变化量，微分方程就是根据变化量列的方程。
• 例子
  • DE 用于描述种群（例如兔群与狼群）数量为什么增加，为什么减少这样一种变化，比描述某一点的特定值更加容易。
    • 你很难去直接列出，种群或者说人口变化的最终，t关于人口的数量的模型
    • 但是你可以通过观察简单的变化量来逆推这个t关于人口的数量的模型
  • 研究单摆的微分方程时，为什么我们先求加速度与角度的关系。因为直接求低维的角度与周期的关系过于的复杂，没法分析下手。越高维，抽象的角度来观测模型，事情便会变得简单。

类型

• 常微分方程 Ordinary Differential Equation, ODE

  • 单变量

    只有一个变量，通常是时间

    

    

• 偏微分方程 Partial Differential Equation, PDE

  • 多变量

    有多个输入变量

    

    

可以把 微分方程 DE，想象成一个随时间变化的连续体/连续集合

导入

空中物体的运动轨迹

• 关于重力加速度 \(g\) 的简单 DE

  我们用 \(y(t)\) 来描述物体的关于时间与位移的关系

  

  而这个物体持续受到向下的重力加速度 \(-g\)，即 \(-g\)

  为了方便表达，我们将 \(y(t)\) 的一阶导数写为 \(\dot{y}(t)\)，二阶导同理 \(\ddot{y}(t)\)

  所以我们的微分方程可以表达为 \(\ddot{y}(t) = -g\)

  求解过程就是一个简单的求不定积分的过程

  \[\ddot{y}(t) = -g \\ \frac{d^2(?)}{d^2t}(t) = -g \\ \frac{d(?)}{dt} = -gt + v_0 \\ \frac{d(-\frac12gt^2 + v_0t + c1)}{dt} = -gt + v_0 \\ y(t) = -\frac12gt^2 + v_0t + c1\]

解 ODE 的目的

• 目的

  • 不难发现，解 ODE 的问题基本都是去寻找到 高阶函数 逐渐向前递推寻找原函数的过程。
  • 在物理学中，最常见的是 二阶常微分方程（Second Order ODE），即表达式中最高阶的导数为二阶导数

  

  

从单摆的简谐运动建立起对微分方程的直观感觉

• 单摆

  单摆，简单和谐运动（Simple Harmonic Motion），不考虑空气阻力和摩擦等非保守力

  当我们以常规视角来观测时，我们会得到以下结论。

  起始角度为小角度时才近似成立：

  • 角度与时间的关系 \(\theta(t) = \theta_0cos(\sqrt{\frac{g}{Lt}})\)，周期 \(2\pi\sqrt{\frac{L}{g}}\)
  • 其中 \(L\) 是摆长， \(g\) 为重力加速度

  我们可以通过构建微分方程来窥探单摆的实际情况

  首先，确定一个最高阶的变换量（因为最高阶的变换量最简单把握），即加速度。

  通过受力分析可以得到 \(a = \ddot{x} = -g\sin(\theta)\)

  

  \[\ddot{x} = L\ddot{\theta}=-g\sin(\theta) \\ \ddot{\theta} = -\frac{g}{L}\sin(\theta)\]

  考虑空气阻力，\(\dot{\theta}\) 为 \(\theta\) 变化的速率，也就是 \(\theta\) 的速度大小

  \[\ddot{\theta}(t) = -\mu\dot{\theta}-\frac{g}{L}sin(\theta)\]

  如果我们可以对他求解的话，就能得到原函数 \(\theta(t)\) 的表达式

  但很显然，解决像是这样的微分方程需要用到像是椭圆积分和不完全椭圆积分这种超级难算的东西。我们不指望把它解出来。

  无法求解，就跳过求解，直接构建对微分方程的理解与计算

  

  我们要理解，就要先构建可视化的图像。

  你可能会想试图构建这个\(\space \theta-t\) 的函数图像，然后去揣测它的位置，斜率，曲率是什么含义。

  但很显然，你很难去联想二阶导受到一阶导影响但这样一个非常魔幻的图像是有什么含义。

  但我们可以尝试把上面的式子，构建 \(\dot{\theta} - \theta\) （影响加速度的两个因子）的图像。这个二维平面上的点，完全描述了任意时刻单摆的状态。

  

  我们便可以画出这个单摆在任意一个初始状态下，开始演变，然后收敛到最后的结果。

  

  从某种意义上来说，这个点就是被原点所吸引。

  我们可以再进一步，将其变成向量场。对单个状态向量进行求导，便可得到变化率，运动趋势。

  

  并且我们可以将求导出来的新向量附加在原有状态上，用于表示运动趋势。

  对于 \(\begin{bmatrix} \dot{\theta}(t) \\ \ddot{\theta}(t) \end{bmatrix}\)这个新向量来说，\(\dot{\theta}(t)\) 可以理解为，角度的变化速度，越高则越倾向右边，越低则越倾向左。 \(\ddot{\theta}(t)\) 可以直接替换为我们之前的式子 \(\ddot{\theta}(t) = -\mu\dot{\theta}-\frac{g}{L}sin(\theta)\)。

  最终便是：

  \[\frac{d}{dt}\begin{bmatrix} \theta(t) \\ \dot{\theta}(t) \end{bmatrix}=\begin{bmatrix} \dot{\theta}(t) \\ \ddot{\theta}(t) \end{bmatrix} = \begin{bmatrix} \dot{\theta}(t) \\ -\mu\dot{\theta}-\frac{g}{L}sin(\theta) \end{bmatrix}\]

  我们便可以得到像这样一张图

  

  你也可以发现，我们将一个二阶ODE分解成了一阶常微分方程组（System of two first order OEDs）

  而且我们观察一下这个 一阶ODE组，不难发现，他们的的变化率是交织在一起的，他们会同时影响自身和对方的变化率。