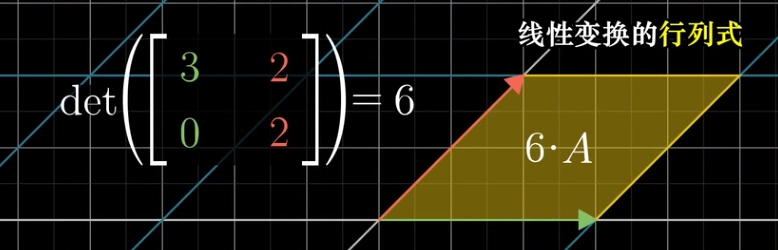本笔记直接从 Notion 签出，格式混乱，内容或有错误，仅供参考

Linear Algebra Introduction

Vector 向量

• 向量，即一组变量 \(\mathbf x = (x_1, x_2, x_3, \cdots ,x_n)\)

Linear Relationship & Linear System of Equations 线性关系与线性方程组

• 线性关系指的是
  • 对输入只进行，“相加”和“数乘” 两种计算方式
• 若存在如下 “线性方程组” 即方程满足线性关系的定义：

\[\begin{cases} \begin{align*} a_{11}x_1 + a_{12} x_2 + &\cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + &\cdots + a_{2n}x_n = b_2 \\ &\vdots \end{align*} \\ a_{n1}x_1 + a_{n2}x_2 + \cdots +a_{nn}x_n = b_n\end{cases}\]

• 而我们可以将其中的系数提出，左边的是输入，右边的是输出，便可以得到

\[\mathbf A = \begin{bmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\end{bmatrix}, \quad\mathbf x = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}, \quad \mathbf b = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m\end{pmatrix}\]

• 其中 \(n\), \(m\) 是向量的纬度
• 如果我们将其视为 矩阵 \(\mathbf A\) 作用在 \(\mathbf x\) 上的输出为 \(\mathbf b\)，则可以将其表示为

\[\mathbf A_{m\times n} \mathbf x_{n} = \mathbf b_{m}\]

Matrix 矩阵

• 由 \(mn\) 个(实或复)数 \(a_{ij}\;(i=1,2,\cdots,m;\,j=1,2,\cdots,n)\) 排成 \(m\) 行 \(n\) 列的阵式(矩形表),称为 \(m\times n\) 矩阵，记为

\[\begin{bmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\end{bmatrix}\]

Operation of Matrix 矩阵的运算

• 矩阵加法就是对应元素相加

\[\mathbf A + \mathbf B = \begin{bmatrix}a_{11} + b_{11} & a_{12}+b_{12} & \cdots & a_{1n} + b_{1n} \\ a_{21}+b_{21} & a_{22}+b_{22} & \cdots & a_{2n} + b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} + b_{m1} & a_{m2} + b_{m2}& \cdots & a_{mn} + b_{mn}\end{bmatrix}\]

• 矩阵数乘就是对应元素与数的乘积

\[\lambda \mathbf A = \begin{bmatrix}\lambda a_{11} & \lambda a_{12} & \cdots & \lambda a_{1n} \\ \lambda a_{21} & \lambda a_{22} & \cdots & \lambda a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \lambda a_{m1} & \lambda a_{m2} & \cdots & \lambda a_{mn}\end{bmatrix}\]

• 用线性方程组的语言表述如下

\[\mathbf Y_1 = \mathbf {AX} \quad \mathbf Y_2 = \mathbf {BX} \\ \mathbf Y = \mathbf Y_1 + \mathbf Y_2 = (\mathbf Y_1 + \mathbf Y_2) = (\mathbf A + \mathbf B) \mathbf X \\ \mathbf Z = \lambda \mathbf Y = (\lambda\mathbf A) \mathbf X\]

• 矩阵乘法

  \[\mathbf A_{n\times p} \mathbf B_{q \times m} = \mathbf B_{m\times n}, \quad s.t. \; p =q\]

• 矩阵的逆，若有如下线性方程组

\[\begin{cases} \begin{align*} a_{11}x_1 + a_{12} x_2 + &\cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + &\cdots + a_{2n}x_n = b_2 \\ &\vdots \end{align*} \\ a_{n1}x_1 + a_{n2}x_2 + \cdots +a_{nn}x_n = b_n\end{cases}\]

• 将其表示为 \(\mathbf A_{m\times n} \mathbf x_{n} = \mathbf b_{m}\)，也就是矩阵 \(\mathbf A\) 作用在 \(\mathbf x\) 上的输出为 \(\mathbf b\)
  • 如果我们反过来看，我们希望获得一个矩阵 \(\mathbf C\) 作用在 \(\mathbf b\) 上反过来可以得到 \(\mathbf x\)，那么我们称矩阵 \(\mathbf C\) 为矩阵 \(\mathbf A\) 的逆，记为 \(\mathbf A^{-1}\)，用数学语言表达如下

\[\mathbf A\mathbf x = \mathbf b \Leftrightarrow \mathbf A \mathbf A^{-1} \mathbf x = \mathbf b \mathbf A^{-1} \\ \mathbf x = \mathbf b\mathbf A^{-1}\]

• 其中 \(\mathbf A \mathbf A^{-1}\) 对 \(\mathbf x\) 没有作用，记为单位矩阵 \(\mathbf E\)，即 \(\mathbf A \mathbf A^{-1} = \mathbf E\)
  • 矩阵可逆当且仅当矩阵的行列式不为 \(0\)，即 \(\det (\mathbf A) \neq 0\)
  • 也就是说当 \(\mathbf A\) 作用在 \(\mathbf x\) 上没有将空间压缩到更低维度即有逆变换 （克莱姆法则）

Linear Combination and Linear Dependent 线性组合和线性相关

• 定义 \(\hat i = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\) \(\hat j = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\)
• 如果我们有基向量 \(\hat i\), \(\hat j\)，我们可以将原有对向量 \(\mathbf x = a + b\) 表示为 \(\mathbf x = a\hat i + b\hat j\)，我们称这样的一种组合叫线性组合

• 如果向量 \(\mathbf u\) 可以被基向量 \(\hat i\), \(\hat j\) 的线性组合所表示即 \(\mathbf u = a\hat i +b\hat j\)，那么就称 \(\mathbf u\) 和 \(\hat i\), \(\hat j\) 是线性相关的
• 如果向量 \(\mathbf u\) 不能被基向量 \(\hat i\), \(\hat j\) 的线性组合所表示即 \(\mathbf u = a\hat i +b\hat j\)，那么就称 \(\mathbf u\) 和 \(\hat i\), \(\hat j\) 是线性无关的
• 我们称基向量 \(\hat i\), \(\hat j\) 所有的线性组合所张的空间为线性空间
• 若向量组的一个子组线性无关,但将向量组中任何一个向量添到这个子组中去得到的都是线性相关的子组,则称该线性无关子组为向量组的极大线性无关组。（也就是说只需要极大线性无关组便可以张成该向量组所张成的线性空间，其余的向量组中的向量都可以被极大线性无关组所表示）
  • 向量组的任何向量都是它的极大线性无关组的线性组合
  • 向量组的极大无关组可能不止一个
  • 对于一个给定的向量组,它的极大线性无关组所含向量的个数相同
  • 由 \(n\) 维向量构成的向量组的极大线性无关组由不超过 \(n\) 个向量组成

Rank and Basis Vector 秩、基向量

• 向量组的极大线性无关组所含向量的个数，称为向量组的秩
  • 一个向量组的所有可能的线性组合构成的集合，就是该向量组的任何极大线性无关组的所有可能的线性组合构成的集合
• 对该集合而言,指定一个极大线性无关组,该极大线性无关组可以称为该集合的一组基

Basis Transformation 基变换

• 坐标轴变换

Linear Transformation and Linear Mapping 线性变化与线性映射

• 若有 \(\mathbf X\), \(\mathbf Y\) 在线性空间 \(\mathbf V\) 中，一个映射（函数）如下

\[\mathbf Y = F(\mathbf X)\]

• 如果 \(f\) 满足
  • 对于 \(\forall \mathbf X_1, \mathbf X_2 \in V \quad \exists F(\mathbf X_1 + \mathbf X_2) = F(\mathbf X_1) + F(\mathbf X_2)\)
  • 对于 \(\forall \mathbf X,\lambda \in V \quad \exists F(\lambda\mathbf X) = \lambda F(\mathbf X)\)
• 则称 \(F\) 是线性空间 \(V\) 上的一个线性变换

Column Space 列空间

• 列空间就是矩阵的列所张成的空间。秩的更精确的定义是列空间的维数。
• 满秩是指输入空间的维度等于矩阵的秩。
  • 对于一个满秩变换来说，唯一能在变换后落在原点的就是零向量自身。
  • 对于非满秩的变换，将维度压缩到更低的维度，也就是说会有一系列的向量会压缩到原点。在变换后落在原点的向量集合，被称为所选矩阵的零空间或核。

Abstract Linear Space 抽象线性空间

• 向量加法满足结合律 \(\mathbf u + (\mathbf v + \mathbf w) = (\mathbf u + \mathbf v) + \mathbf w\)
• 向量加法满足交换律 \(\mathbf v + \mathbf w = \mathbf w + \mathbf v\)
• 向量加法的单位元存在 \(0 + \mathbf v = \mathbf v\)
• 每个向量的加法逆元均存在 \(\mathbf v + (-\mathbf v) = 0\)
• 标量乘法与标量的域乘法相容 \(a(b\mathbf v) = (ab) \mathbf v\)
• 标量乘法的单位元存在 \(1 \mathbf v = \mathbf v\)
• 标量乘法对向量加法满足分配律 \(a(\mathbf v + \mathbf w) = a\mathbf v + a\mathbf w\)
• 标量乘法对域加法满足分配律 \((a + b) \mathbf v = a\mathbf v + b \mathbf v\)
• 只要给定一组基，对抽象线性空间的研究就可以转化为对坐标向量空间，普通加法与数乘的研究，无需关心抽象线性空间的元素形式及其“加法”“数乘”的具体定义。
  • 例如 \(V = \mathbb R^+, F = \mathbb, a \oplus b = ab, k \otimes a = a^k\) 其中 \(V\) 便是线性空间
• “普适的代价是抽象”

Eigenvalues and eigenvectors 特征值与特征向量

• 在线性变换中，有的向量并不改变方向，只是拉伸或者缩小。这些向量就叫特征向量，每个特征向量都有一个所属的值，拉伸倍数叫做特征值。数学语言表达如下

\[\mathbf A\mathbf X = \lambda \mathbf X \Leftrightarrow (\mathbf A - \lambda \mathbf E)\mathbf X = 0\]

• 如果上述方程有非零解，那么就存在特征向量，其中 \(\lambda \mathbf E\) 将拉伸倍数乘单位矩阵，使得其转化为矩阵，这样才可以做矩阵运算。
• 根据行列式相关计算性质，上式可以化为一个关于\(\mathbf A\) 的一元 \(n\) 次方程,即可求出可能的特征值
  • 最后将每个特征值代入回线性方程组，可以解出对应的特征向量。

Eigenvalues and Determinant 特征值与行列式

• 图形经过变换后的面积（或体积，或超体积）与之前面积（或体积，或超体积）的比。

\[|\mathbf A| = \lambda_1 \lambda_2 \cdots \lambda_n\]

Application of Linear Algebra 线性代数的应用

• 降维
  • 一个三维空间中的平面是二维的，但其上每个点的坐标依然有三个分量。
  • 数据的降维,即是指去除与数据分布无关的变量自由度的过程
  • 用最少的独立取值的变量数量描述数据的变化
  • 主成分分析（PCA）

• 傅立叶变换
  • 任何一个一维周期函数都可以表示为一组正弦函数的线性组合：它们的周期（频率）的比值为整数比。
  • 可以证明，这组正弦函数构成了给定周期值的所有分段光滑周期函数的集合的一组基。
  • 我们把原始周期函数称为位于“时域”，把按正弦基函数分解所获得的坐标-频率函数称为位于“频域”
  • 推广到非周期函数时，频域的自变量取值由离散变成连续。进一步地，可以推广到任意维上的函数。

• 图像滤波
  • 对于傅里叶变换而言,时域卷积等同于频域相乘(滤波)
  • 在图像上所做的卷积操作本质是对图像进行某种形式的滤波 (卷积网络中便是对基的选择进行学习)
  • 所谓的 feature vector, 本质上更加接近于选定了某些基后在该基下的坐标。

• 矩阵微分
  • 考虑多元函数 \(f(x_1, x_2, x_3)\)，其梯度为

\[\nabla f = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n}\end{bmatrix} = (\frac{\partial f}{\partial \mathbf x})^{\mathsf T}\]

\[\frac{\partial \mathbf y}{\partial x} = \begin{bmatrix} \frac{\partial y_1}{\partial x} \\ \frac{\partial y_2}{\partial x} \\ \vdots \\ \frac{\partial y_n}{\partial x}\end{bmatrix} \cdot \frac{\partial y}{\partial \mathbb x} = \begin{bmatrix} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2} & \cdots & \frac{\partial f}{\partial x_n}\end{bmatrix} \cdot \frac{\partial \mathbf y}{ \mathbf x} = \begin{bmatrix}\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n}\end{bmatrix}\]