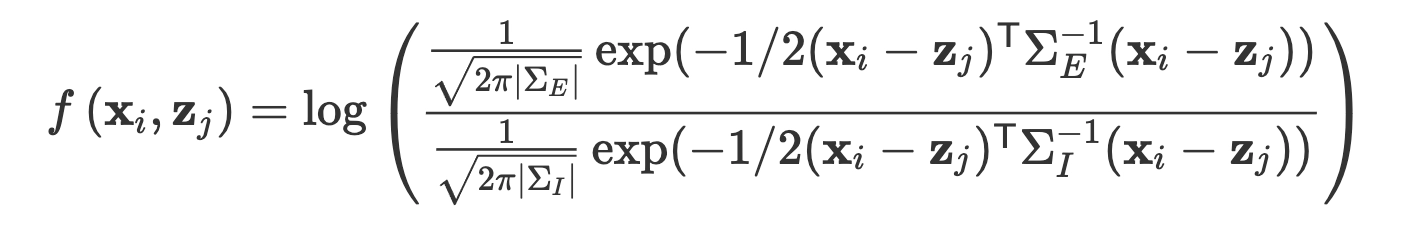相关工作 马氏距离，即 Mahalanobis Distance KISSME 方法，全称
Keep It Simple and Straightforward Metric
即保持直接简单原则的度量方法，属于有监督的线性度量学习方法，本质上还是学习马氏距离中的矩阵
XQDA+LOMO 方法，交叉视角的二次判别分析算法是基于
KISSME 提出的改进算法，使用 LOMO
特征提取的方法，再通过 LDA
算法投影到度量子空间用于降维，再进行马氏距离度量。马氏距离 Mahalanobis
Distance 标准马氏距离通过引入协方差矩阵，使得其度量出考虑属性之间相关性且尺度无关的距离 d ( x i , x j ) = ∥ x i − x j ∥ Σ − 1 2 = ( x i − x j ) T Σ − 1 ( x i − x j )
d(\mathbf{x}_i, \mathbf{x}_j) = \left\| \mathbf{x}_i - \mathbf{x}_j
\right\|_{\Sigma ^{-1}}^{2} = (\mathbf{x}_i - \mathbf{x}_j)^{\mathsf{T}}
\Sigma ^{-1}(\mathbf{x}_i - \mathbf{x}_j)
d ( x i , x j ) = ∥ x i − x j ∥ Σ − 1 2 = ( x i − x j ) T Σ − 1 ( x i − x j )
而通用马氏距离则通过一个通用的度量矩阵 M \mathbf{M} M M \mathbf{M} M d ( x i , x j ) = ∥ x i − x j ∥ M 2 = ( x i − x j ) T M ( x i − x j )
d(\mathbf{x}_i, \mathbf{x}_j) = \left\| \mathbf{x}_i - \mathbf{x}_j
\right\|_{\mathbf{M}}^{2} = (\mathbf{x}_i - \mathbf{x}_j)^{\mathsf{T}}
\mathbf{M}(\mathbf{x}_i - \mathbf{x}_j)
d ( x i , x j ) = ∥ x i − x j ∥ M 2 = ( x i − x j ) T M ( x i − x j )
KISSME 方法 首先，认为对于样本对 ( x i , z j ) (\mathbf{x}_i,\mathbf{z}_j) ( x i , z j ) f ( x i , z j ) = log ( p ( x i − z j ∣ H 0 ) p ( x i − z j ∣ H 1 ) ) f\left(\mathbf{x}_i,\mathbf{z}_j\right)=\log{\left(\frac{p\left(\mathbf{x}_i-\mathbf{z}_j|H_0\right)}{p\left(\mathbf{x}_i-\mathbf{z}_j|H_1\right)}\right)}
f ( x i , z j ) = log ( p ( x i − z j ∣ H 1 ) p ( x i − z j ∣ H 0 ) )
其中，H 0 H_0 H 0 H 1 H_1 H 1 f ( x i , z j ) f(\mathbf{x}_i, \mathbf{z}_j) f ( x i , z j ) H 0 H_0 H 0 f ( x i , z j ) f(\mathbf{x}_i, \mathbf{z}_j) f ( x i , z j ) 假设样本差向量符合 0 0 0 f ( x i , z j ) = log ( 1 2 π ∣ Σ E ∣ exp ( − 1 / 2 ( x i − z j ) T Σ E − 1 ( x i − z j ) ) 1 2 π ∣ Σ I ∣ exp ( − 1 / 2 ( x i − z j ) T Σ I − 1 ( x i − z j ) ) )
f\left(\mathbf{x}_i,\mathbf{z}_j\right)= \log \left(
\frac{\frac{1}{\sqrt{2\pi |\Sigma_E|}} \exp (-1/2
(\mathbf{x}_i-\mathbf{z}_j)^\mathsf{T}
\Sigma^{-1}_E(\mathbf{x}_i-\mathbf{z}_j))}{\frac{1}{\sqrt{2\pi
|\Sigma_I|}} \exp (-1/2 (\mathbf{x}_i-\mathbf{z}_j)^\mathsf{T}
\Sigma^{-1}_I(\mathbf{x}_i-\mathbf{z}_j))}\right)
f ( x i , z j ) = log ⎝ ⎛ 2 π ∣ Σ I ∣ 1 exp ( − 1/2 ( x i − z j ) T Σ I − 1 ( x i − z j )) 2 π ∣ Σ E ∣ 1 exp ( − 1/2 ( x i − z j ) T Σ E − 1 ( x i − z j )) ⎠ ⎞
f ( x i − z j ) = ( x i − z j ) T Σ I − 1 ( x i − z j ) + log ( ∣ Σ I − 1 ∣ ) − ( x i − z j ) T Σ E − 1 ( x i − z j ) − log ( ∣ Σ E − 1 ∣ )
\begin{split}f(\mathbf{x}_{i}-\mathbf{z}_{j}) =
{} &(\mathbf{x}_{i}-\mathbf{z}_{j})^{\mathsf{T}}\Sigma^{-1}_{I}(\mathbf{x}_{i}-\mathbf{z}_{j})+\log(\left|
\Sigma^{-1}_{I}\right|)-{}
\\&(\mathbf{x}_{i}-\mathbf{z}_{j})^{\mathsf{T}}\Sigma^{-1}_{E}(\mathbf{x}_{i}-\mathbf{z}_{j})-\log(\left|
\Sigma^{-1}_{E} \right| )\end{split}
f ( x i − z j ) = ( x i − z j ) T Σ I − 1 ( x i − z j ) + log ( ∣ ∣ Σ I − 1 ∣ ∣ ) − ( x i − z j ) T Σ E − 1 ( x i − z j ) − log ( ∣ ∣ Σ E − 1 ∣ ∣ )
f ( x i , z j ) = ( x i − z j ) T ( Σ I − 1 − Σ E − 1 ) ( x i − z j )
f\left(\mathbf{x}_i,\mathbf{z}_j\right)=
(\mathbf{x}_i-\mathbf{z}_j)^{\mathsf{T}}(\Sigma^{-1}_{I} -
\Sigma^{-1}_{E})(\mathbf{x}_i-\mathbf{z}_j)
f ( x i , z j ) = ( x i − z j ) T ( Σ I − 1 − Σ E − 1 ) ( x i − z j )
最后便得到了反映了对数似然比检验属性的马氏距离度量 d ( x i , z j ) = ( x i − z j ) T M ( x i − z j ) = ( x i − z j ) T ( Σ I − 1 − Σ E − 1 ) ( x i − z j ) d(\mathbf{x}_i,
\mathbf{z}_j)=(\mathbf{x}_i-\mathbf{z}_j)^{\mathsf{T}}\mathbf{M}(\mathbf{x}_i-\mathbf{z}_j)
= (\mathbf{x}_i-\mathbf{z}_j)^{\mathsf{T}}(\Sigma^{-1}_{I} -
\Sigma^{-1}_{E})(\mathbf{x}_i-\mathbf{z}_j) d ( x i , z j ) = ( x i − z j ) T M ( x i − z j ) = ( x i − z j ) T ( Σ I − 1 − Σ E − 1 ) ( x i − z j )
上述的 KISSME
方法主要利用假设检验的思想，建立一个正负样本对概率的似然比函数作为统计量，使得正负样本分布服从两个不同的参数的高斯分布，学习一个马氏距离的
M \mathbf{M} M XQDA + LOMO 方法 LOMO 是一种特征提取手段，不多赘述。
XQDA 则在 KISSME 方法上更近一步，使用
QDA
方法，学习一个具有辨别力的子空间，然后再用马氏距离进行度量。
所以重新构造似然比函数，其中 W \mathbf{W} W ( x i , z j ) (\mathbf{x}_i,\mathbf{z}_j) ( x i , z j )
f ( x i , z j ) = log ( p ( W T x i − W T z j ∣ H 0 ) p ( W T x i − W T z j ∣ H 1 ) ) f\left(\mathbf{x}_i,\mathbf{z}_j\right)=\log{\left(\frac{p\left(\mathbf{W}^{\mathsf{T}}\mathbf{x}_i-\mathbf{W}^{\mathsf{T}}\mathbf{z}_j|H_0\right)}{p\left(\mathbf{W}^{\mathsf{T}}\mathbf{x}_i-\mathbf{W}^{\mathsf{T}}\mathbf{z}_j|H_1\right)}\right)}
f ( x i , z j ) = log ( p ( W T x i − W T z j ∣ H 1 ) p ( W T x i − W T z j ∣ H 0 ) )
f ( x i − z j ) = W ( x i − z j ) T Σ I − 1 ( x i − z j ) W T + log ( ∣ Σ I − 1 ∣ ) − W ( x i − z j ) T Σ E − 1 ( x i − z j ) W T − log ( ∣ Σ E − 1 ∣ ) \begin{split}f(\mathbf{x}_{i}-\mathbf{z}_{j}) =
{} &\mathbf{W}(\mathbf{x}_{i}-\mathbf{z}_{j})^{\mathsf{T}}\Sigma^{-1}_{I}(\mathbf{x}_{i}-\mathbf{z}_{j})\mathbf{W}^{\mathsf{T}}+\log(\left|
\Sigma^{-1}_{I}\right|)-{} \\
&\mathbf{W}(\mathbf{x}_{i}-\mathbf{z}_{j})^{\mathsf{T}}\Sigma^{-1}_{E}(\mathbf{x}_{i}-\mathbf{z}_{j})\mathbf{W}^{\mathsf{T}}-\log(\left|
\Sigma^{-1}_{E} \right| )\end{split} f ( x i − z j ) = W ( x i − z j ) T Σ I − 1 ( x i − z j ) W T + log ( ∣ ∣ Σ I − 1 ∣ ∣ ) − W ( x i − z j ) T Σ E − 1 ( x i − z j ) W T − log ( ∣ ∣ Σ E − 1 ∣ ∣ )
f ( x i , z j ) = W ( x i − z j ) T ( Σ I − 1 − Σ E − 1 ) ( x i − z j ) W T
f\left(\mathbf{x}_i,\mathbf{z}_j\right)=
\mathbf{W}(\mathbf{x}_i-\mathbf{z}_j)^{\mathsf{T}}(\Sigma^{-1}_{I} -
\Sigma^{-1}_{E})(\mathbf{x}_i-\mathbf{z}_j)\mathbf{W}^{\mathsf{T}}
f ( x i , z j ) = W ( x i − z j ) T ( Σ I − 1 − Σ E − 1 ) ( x i − z j ) W T
利用 LDA
方法的思想，对行人的分类可以表示为一个多分类的LDA投影子空间学习任务，计算类内和类间散度 { S w = 1 N ∑ i = 1 C ∑ j = 1 N i ( y i , j − y ‾ i ) ( y i , j − y ‾ i ) T S b = 1 C ∑ i = 1 C ( y ‾ i − y ‾ ) ( y ‾ i − y ‾ ) T \begin{cases} \mathbf{S}_{w} =
\displaystyle\frac{1}{N}\displaystyle\sum_{i=1}^{C}
\displaystyle\sum_{j=1}^{N_i}
(\mathbf{y}_{i,j}-\overline{\mathbf{y}}_{i})(\mathbf{y}_{i,j}-\overline{\mathbf{y}}_{i})^{\mathsf{T}}
\\ \mathbf{S}_b = \displaystyle\frac{1}{C}
\displaystyle\sum_{i=1}^{C}
(\overline{\mathbf{y}}_{i}-\overline{\mathbf{y}})(\overline{\mathbf{y}}_{i}-\overline{\mathbf{y}})^{\mathsf{T}}\end{cases} ⎩ ⎨ ⎧ S w = N 1 i = 1 ∑ C j = 1 ∑ N i ( y i , j − y i ) ( y i , j − y i ) T S b = C 1 i = 1 ∑ C ( y i − y ) ( y i − y ) T
max J ( w ) = w T S b w w T S w w \max{J}(\mathbf{w})=\frac{\mathbf{w}^{\mathsf{T}}\mathbf{S}_b\mathbf{w}}{\mathbf{w}^{\mathsf{T}}\mathbf{S}_w\mathbf{w}} max J ( w ) = w T S w w w T S b w
转化为广义瑞利商函数的相关性质可知，对于上述模型的最优化可以转化为如下特征根分解的问题 S w − 1 S b w = λ w \mathbf{S}_w^{-1}\mathbf{S}_b\mathbf{w}=\lambda\mathbf{w}
S w − 1 S b w = λ w
求解得到的特征向量中，对应特征根值最大的特征向量对应上述优化模型的最优解
w 1 \mathbf{w}_1 w 1 J ( w ) J(\mathbf{w}) J ( w ) J ( w ) J(\mathbf{w}) J ( w ) r r r W = ( w 1 , w 2 , ⋯ , w r ) \mathbf{W}=\left(\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_r\right) W = ( w 1 , w 2 , ⋯ , w r )
XQDA
主要通过学习一个具有辨别力的子空间，最后在使用马氏距离度量投影到子空间后的距离。基于样本相似性和参考集约束的改进 基于正样本分布距离的约束 首先，目前模型的可以正确的识别出部分样本，并且在训练集上表现良好，只是在测试集上过拟合现象较为严重。
一个有效的度量模型，在训练集和测试集的正样本之间的距离分布应该一致。
所以我们假定数据集 A ′ = { x 1 ′ , x 2 ′ , ⋯ , x i ′ , ⋯ , x N ′ ′ } , B ′ = { z 1 ′ , z 2 ′ , ⋯ , z j ′ , ⋯ , z N ′ ′ } \mathbf{A}^\prime=\left\{\mathbf{x}_1^\prime,\mathbf{x}_2^\prime,\cdots,\mathbf{x}_i^\prime,\cdots,\mathbf{x}_{N^\prime}^\prime\right\},
\mathbf{B}^\prime=\left\{\mathbf{z}_1^\prime,\mathbf{z}_2^\prime,\cdots,
\mathbf{z}_j^\prime,\cdots,\mathbf{z}_{N^\prime}^\prime\right\} A ′ = { x 1 ′ , x 2 ′ , ⋯ , x i ′ , ⋯ , x N ′ ′ } , B ′ = { z 1 ′ , z 2 ′ , ⋯ , z j ′ , ⋯ , z N ′ ′ }
基于已经训练了的 XQDA 模型，在测试集 B ′ \mathbf{B}' B ′ k k k
v i = x i ′ − z i ′ = 1 k ∑ i = 1 N q i j α i j ( x i ′ − z j )
\mathbf{v}_i=\mathbf{x}_i^\prime-\mathbf{z}_i^\prime=\frac{1}{k}\sum_{i=1}^{N}{q_{ij}\alpha_{ij}\left(\mathbf{x}_i^\prime-\mathbf{z}_j\right)}
v i = x i ′ − z i ′ = k 1 i = 1 ∑ N q ij α ij ( x i ′ − z j )
其中 q i j q_{ij} q ij α i j \alpha_{ij} α ij ( x i ′ , z j ′ ) (\mathbf{x}_i',\mathbf{z}_j') ( x i ′ , z j ′ ) α i j = { 1 − d ( x i ′ , z j ′ ) ∑ q i j ( x i ′ , z j ′ ) q i j = 1 0 q i j = 0
\alpha_{ij}=\begin{cases}
1-\frac{d(x^{^\prime}_i,z^{\prime}_j)}{\sum
q_{ij}(x^{^\prime}_i,z^{\prime}_j)} & q_{ij}=1
\\
0 & q_{ij}=0
\end{cases}
α ij = ⎩ ⎨ ⎧ 1 − ∑ q ij ( x i ′ , z j ′ ) d ( x i ′ , z j ′ ) 0 q ij = 1 q ij = 0
u = 1 N ∑ i = 1 N ( x i − z i )
\mathbf{u}=\frac{1}{N}\sum_{i=1}^{N}\left(\mathbf{x}_i-\mathbf{z}_i\right)
u = N 1 i = 1 ∑ N ( x i − z i )
S = 1 N ′ ∑ i = 1 N ′ ∥ w T v i − w T u ∥ 2 2 = 1 N ′ ∑ i = 1 N ′ w T ( v i − u ) ( v i − u ) T w = 1 N ′ w T ∑ i = 1 N ′ ( v i − u ) ( v i − u ) T w = 1 N ′ w T S ′ w
\begin{aligned}
\mathbf{S} &= \frac{1}{N^\prime}\sum_{i=1}^{N^\prime}\left\|
\mathbf{w}^{\mathsf{T}}\mathbf{v}_{i}-\mathbf{w}^{\mathsf{T}}\mathbf{u}
\right\|_{2}^{2} \\
&=\frac{1}{N^\prime}\sum_{i=1}^{N^\prime}
\mathbf{w}^{\mathsf{T}}(\mathbf{v}_{i}-\mathbf{u})(\mathbf{v}_{i}-\mathbf{u})^{\mathsf{T}}\mathbf{w}
\\
&= \frac{1}{N^\prime} \mathbf{w}^{\mathsf{T}}
\sum_{i=1}^{N^\prime}
(\mathbf{v}_{i}-\mathbf{u})(\mathbf{v}_{i}-\mathbf{u})^{\mathsf{T}}\mathbf{w}
\\
&=
\frac{1}{N^\prime}\mathbf{w}^{\mathsf{T}}\mathbf{S}^\prime\mathbf{w}
\end{aligned}
S = N ′ 1 i = 1 ∑ N ′ ∥ ∥ w T v i − w T u ∥ ∥ 2 2 = N ′ 1 i = 1 ∑ N ′ w T ( v i − u ) ( v i − u ) T w = N ′ 1 w T i = 1 ∑ N ′ ( v i − u ) ( v i − u ) T w = N ′ 1 w T S ′ w
基于负样本与参考集距离的约束 我们定义一个参考集 C = B \mathbf{C} =
\mathbf{B} C = B B \mathbf{B} B
测试数据 A ′ \mathbf{A}' A ′ C \mathbf{C} C
一个有效的度量模型，A ′ \mathbf{A}' A ′ C \mathbf{C} C
因为测试集标签数据是不可知的，所以我们基于已经训练了的
XQDA 模型，在测试集 B ′ \mathbf{B}' B ′ k ′ k' k ′
所以我们定义参考集负样本于测试集负样本差异如下
D = ∥ w T ( 1 N A ′ N C ∑ n = 1 N A ′ ∑ j = 1 N C ( x i ′ − z j ) ) − w T ( 1 N A ′ N B ′ ∑ s = 1 N A ′ ∑ t = 1 N B ′ p s t ( x s − z t ) ) ∥ 2 2
\mathbf{D} = \left\| \mathbf{w}^{\mathsf{T}}\left( \frac{1}{N_{A'}
N_{C}} \sum\limits_{n=1}^{N_{A'}} \sum\limits_{j=1}^{N_C} \left(
\mathbf{x}'_i - \mathbf{z}_j \right) \right) -
\mathbf{w}^{\mathsf{T}}\left(
\frac{1}{N_{A'}N_{B'}}\sum\limits_{s=1}^{N_{A'}}
\sum\limits_{t=1}^{N_{B'}} p_{st}(\mathbf{x}_s - \mathbf{z}_t)
\right) \right\|_{2}^{2}
D = ∥ ∥ w T ⎝ ⎛ N A ′ N C 1 n = 1 ∑ N A ′ j = 1 ∑ N C ( x i ′ − z j ) ⎠ ⎞ − w T ⎝ ⎛ N A ′ N B ′ 1 s = 1 ∑ N A ′ t = 1 ∑ N B ′ p s t ( x s − z t ) ⎠ ⎞ ∥ ∥ 2 2
其中 ( 1 N A ′ N C ∑ n = 1 N A ′ ∑ j = 1 N C ( x i ′ − z j ) ) \left( \frac{1}{N_{A'}
N_{C}} \sum\limits_{n=1}^{N_{A'}} \sum\limits_{j=1}^{N_C} \left(
\mathbf{x}'_i - \mathbf{z}_j \right) \right) ( N A ′ N C 1 n = 1 ∑ N A ′ j = 1 ∑ N C ( x i ′ − z j ) )
( 1 N A ′ N B ′ ∑ s = 1 N A ′ ∑ t = 1 N B ′ p s t ( x s − z t ) ) \left(
\frac{1}{N_{A'}N_{B'}}\sum\limits_{s=1}^{N_{A'}}
\sum\limits_{t=1}^{N_{B'}} p_{st}(\mathbf{x}_s - \mathbf{z}_t)
\right) ( N A ′ N B ′ 1 s = 1 ∑ N A ′ t = 1 ∑ N B ′ p s t ( x s − z t ) )
p s t p_{st} p s t x s \mathbf{x}_s x s z t \mathbf{z}_t z t x s ∈ A ′ , z t ∈ B ′ \mathbf{x}_s \in \mathbf{A}', \mathbf{z}_t \in
\mathbf{B}' x s ∈ A ′ , z t ∈ B ′
展开上式
D = ∥ w T ( 1 N A ′ N C ∑ n = 1 N A ′ ∑ j = 1 N C ( x i ′ − z j ) ) − w T ( 1 N A ′ N B ′ ∑ s = 1 N A ′ ∑ t = 1 N B ′ p s t ( x s − z t ) ) ∥ 2 2 = [ t ] w T ( 1 N A ′ N C ∑ n = 1 N A ′ ∑ j = 1 N C ( x i ′ − z j ) − 1 N A ′ N B ′ ∑ s = 1 N A ′ ∑ t = 1 N B ′ p s t ( x s − z t ) ) ( 1 N A ′ N C ∑ n = 1 N A ′ ∑ j = 1 N C ( x i ′ − z j ) − 1 N A ′ N B ′ ∑ s = 1 N A ′ ∑ t = 1 N B ′ p s t ( x s − z t ) ) T w = w T D ′ w
\begin{aligned}
\mathbf{D} &= \left\| \mathbf{w}^{\mathsf{T}}\left(
\frac{1}{N_{A'} N_{C}} \sum\limits_{n=1}^{N_{A'}}
\sum\limits_{j=1}^{N_C} \left( \mathbf{x}'_i - \mathbf{z}_j
\right) \right) - \mathbf{w}^{\mathsf{T}}\left(
\frac{1}{N_{A'}N_{B'}}\sum\limits_{s=1}^{N_{A'}}
\sum\limits_{t=1}^{N_{B'}} p_{st}(\mathbf{x}_s - \mathbf{z}_t)
\right) \right\|_{2}^{2} \\
&=\begin{aligned}[t]
&\mathbf{w}^{\mathsf{T}}\left( \frac{1}{N_{A'} N_{C}}
\sum\limits_{n=1}^{N_{A'}} \sum\limits_{j=1}^{N_C} \left(
\mathbf{x}'_i - \mathbf{z}_j \right) -
\frac{1}{N_{A'}N_{B'}}\sum\limits_{s=1}^{N_{A'}}
\sum\limits_{t=1}^{N_{B'}} p_{st}(\mathbf{x}_s - \mathbf{z}_t)
\right) \\ &\left( \frac{1}{N_{A'} N_{C}}
\sum\limits_{n=1}^{N_{A'}} \sum\limits_{j=1}^{N_C} \left(
\mathbf{x}'_i - \mathbf{z}_j \right) -
\frac{1}{N_{A'}N_{B'}}\sum\limits_{s=1}^{N_{A'}}
\sum\limits_{t=1}^{N_{B'}} p_{st}(\mathbf{x}_s - \mathbf{z}_t)
\right)^{\mathsf{T}}\mathbf{w}
\end{aligned}\\
&=\mathbf{w}^{\mathsf{T}}\mathbf{D}'\mathbf{w}
\end{aligned}
D = ∥ ∥ w T ⎝ ⎛ N A ′ N C 1 n = 1 ∑ N A ′ j = 1 ∑ N C ( x i ′ − z j ) ⎠ ⎞ − w T ⎝ ⎛ N A ′ N B ′ 1 s = 1 ∑ N A ′ t = 1 ∑ N B ′ p s t ( x s − z t ) ⎠ ⎞ ∥ ∥ 2 2 = [ t ] w T ⎝ ⎛ N A ′ N C 1 n = 1 ∑ N A ′ j = 1 ∑ N C ( x i ′ − z j ) − N A ′ N B ′ 1 s = 1 ∑ N A ′ t = 1 ∑ N B ′ p s t ( x s − z t ) ⎠ ⎞ ⎝ ⎛ N A ′ N C 1 n = 1 ∑ N A ′ j = 1 ∑ N C ( x i ′ − z j ) − N A ′ N B ′ 1 s = 1 ∑ N A ′ t = 1 ∑ N B ′ p s t ( x s − z t ) ⎠ ⎞ T w = w T D ′ w
改进后的最优化模型 max J ( w ) = w T ( S b + D ′ ) w w T ( S w + α S ′ ) w
\max{J}(\mathbf{w})=\frac{\mathbf{w}^{\mathsf{T}}(\mathbf{S}_b +
\mathbf{D}^{\prime})\mathbf{w}}{\mathbf{w}^{\mathsf{T}}(\mathbf{S}_w+\alpha
\mathbf{S}^{\prime})\mathbf{w}}
max J ( w ) = w T ( S w + α S ′ ) w w T ( S b + D ′ ) w
( S w + α S ′ ) − 1 ( S b + D ′ ) w = λ w
\left(\mathbf{S}_w+\alpha \mathbf{S}^\prime\right)^{-1}(\mathbf{S}_b +
\mathbf{D}')\mathbf{w}=\lambda\mathbf{w}
( S w + α S ′ ) − 1 ( S b + D ′ ) w = λ w
实验 测试数据 VIPeR 是一个基准数据集非重叠，不同时 632 632 632 1264 1264 1264 128 × 48 128 \times 48 128 × 48 包含各种行人步态的变化、背景的变化、照明条件的变化和各种
拍摄角度的变化，数据集很符合实际的应用场景。 使用 50 % 50\% 50% 50 % 50\% 50% 316 316 316 632 632 632 VIPeR
数据集样例评价指标 行人再试别任务中广泛使用的累计精度曲线 CMC 作为评价指标 CMC ( l ) = 1 N ∑ i = 1 N I ( rank ( P i ) < l ) \operatorname{CMC}(l)=\frac{1}{N}\sum_{i=1}^{N}{\mathbb{I}(\operatorname{rank}(P_i)<l)} CMC ( l ) = N 1 i = 1 ∑ N I ( rank ( P i ) < l )
其中，CMC ( l ) \operatorname{CMC}(l) CMC ( l ) l l l rank ( P i ) \operatorname{rank}(P_i) rank ( P i ) i i i I ( ⋅ ) \mathbb{I}(\cdot) I ( ⋅ ) rank ( P i ) \operatorname{rank}(P_i) rank ( P i ) l l l I ( ⋅ ) = 1 \mathbb{I}(\cdot)=1 I ( ⋅ ) = 1 I ( ⋅ ) = 0 \mathbb{I}(\cdot)=0 I ( ⋅ ) = 0 简而言之，rank n 前面能识别正确的百分比，比如
rank 5 就是 前 5 5 5 结果分析 使用刚刚提到 VIPeR 数据进行测试，结果取 10 10 10 精度对比
相较于基线算法 XQDA，提升了 29.63 % 29.63\% 29.63% 不同训练样本规模下的识别精度对比 在训练集 316 316 316 200 200 200 150 150 150 200 200 200 rank 1 在 63 % 63\% 63% 150 150 150 rank 1 在 59 % 59\% 59% 不同维度的精度对比 如图可以看到，使用不同维度的投影矩阵，特征维度在 100 100 100 220 220 220 投影特征维度与矩阵分解时矩阵的维度相关，矩阵越小，则对应的计算效率越高。由此可以看出，算法对于特征维度有很高的鲁棒性，对于算法实时检测有很重要的作用，尤其是在边缘计算，比如摄像头可以直接使用边缘计算芯片，实时处理好了直接发给数据中心。 样本距离分布对比 可以看到相较于 XQDA
基线算法，优化后的算法在过拟合的问题上有显著的缓解。 
